A computer can make a choice between different alternatives based on assigned statistical “likelihoods”—relative probabilities assigned to each possible alternative. This is accomplished most easily by storing all of the probabilities in a single vector (array), calculating the sum of all those probabilities, dividing the range (0 to the sum) into “quantiles” (subranges) proportional to the different probabilities, choosing a random number within that range, and determining which quantile the random number falls into.
The article “Probability distribution” describes this process and shows how to accomplish it, both conceptually (in a prose description that could be implemented as a program) and with an example written in Max using the table object. That article also discusses the implications and limitations of making decisions in this way.
What follows is an example of how to implement a probabilistic decision making program in JavaScript, and a simple Max patch for testing it. I chose to write the example in JavaScript for two reasons. One reason is that JavaScript is an easy-to-understand language, comprehensible to people who already know Java or C; the other reason is just to demonstrate how easy it is to write and use JavaScript code inside Max.
First, let’s recap the process we’ll follow, as stated in that article.
1. Construct a probability vector.
2. Calculate the sum of all probabilities.
3. Choose a random (nonnegative) number less than the sum.
4. Begin cumulatively adding individual probability values, checking after each addition to see if it has resulted in a value greater than the randomly chosen number.
5. When the randomly chosen value has been exceeded, choose the event that corresponds to the most recently added probability.
To see an implementation of this in JavaScript for use in the Max js object, download the file “probabilisticchoice.js” and save it with that name somewhere in the Max file search path. The comments in that file explain what’s being done. In this implementation, though, we use a reverse procedure from the one described in step 4 above. We start by subtracting the value of the last probability in the array from the total sum, and checking to see if that value is less than the random number we chose. If not, we proceed to the next-to-last probability, subtract that, and see if it’s less than the random number, and so on. The principle is the same, we’re just checking downward from the maximum rather than upward from the minimum.
You can try out the program using the example Max patch shown below.
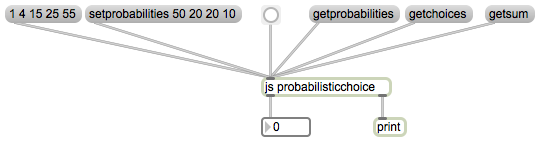
probabilitiestester.maxpat
The JavaScript program accommodates the six input messages shown in the patch. To set the array of probabilities, one can use the setprobabilities message or simply a list. One can query the contents of the variables probabilities, choices, and sum variables, which are sent out the right outlet. The message bang makes a probabilistic choice based on the specified probabilities, and sends the choice (some number from 0 to choices-1) out the left outlet. Note that this is nearly identical to the probabilistic choice capabilities of the table object. It’s shown here as a JavaScript to demonstrate the calculation explicitly.