I have posted an Xcode project for a bare-bones iOS app called Oscillator. It plays a sine tone and allows the user to adjust the amplitude and the frequency (exponentially from -40 dB to 0 dB and from A-110 Hz to A-1760 Hz). It’s not very sophisticated conceptually, technically, or aesthetically, but it does demonstrate the basics of a) mapping user interface objects to methods, b) writing an audio callback function, and c) implementing wavetable synthesis. There’s a fair bit of commentary in the .h and .m files.
Category Archives: Example
Probability distribution vector
A computer can make a choice between different alternatives based on assigned statistical “likelihoods”—relative probabilities assigned to each possible alternative. This is accomplished most easily by storing all of the probabilities in a single vector (array), calculating the sum of all those probabilities, dividing the range (0 to the sum) into “quantiles” (subranges) proportional to the different probabilities, choosing a random number within that range, and determining which quantile the random number falls into.
The article “Probability distribution” describes this process and shows how to accomplish it, both conceptually (in a prose description that could be implemented as a program) and with an example written in Max using the table object. That article also discusses the implications and limitations of making decisions in this way.
What follows is an example of how to implement a probabilistic decision making program in JavaScript, and a simple Max patch for testing it. I chose to write the example in JavaScript for two reasons. One reason is that JavaScript is an easy-to-understand language, comprehensible to people who already know Java or C; the other reason is just to demonstrate how easy it is to write and use JavaScript code inside Max.
First, let’s recap the process we’ll follow, as stated in that article.
1. Construct a probability vector.
2. Calculate the sum of all probabilities.
3. Choose a random (nonnegative) number less than the sum.
4. Begin cumulatively adding individual probability values, checking after each addition to see if it has resulted in a value greater than the randomly chosen number.
5. When the randomly chosen value has been exceeded, choose the event that corresponds to the most recently added probability.
To see an implementation of this in JavaScript for use in the Max js object, download the file “probabilisticchoice.js” and save it with that name somewhere in the Max file search path. The comments in that file explain what’s being done. In this implementation, though, we use a reverse procedure from the one described in step 4 above. We start by subtracting the value of the last probability in the array from the total sum, and checking to see if that value is less than the random number we chose. If not, we proceed to the next-to-last probability, subtract that, and see if it’s less than the random number, and so on. The principle is the same, we’re just checking downward from the maximum rather than upward from the minimum.
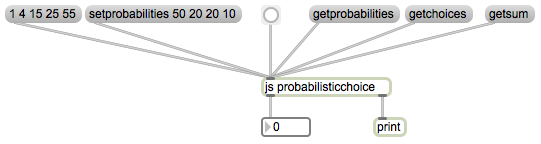
You can try out the program using the example Max patch shown below.
The JavaScript program accommodates the six input messages shown in the patch. To set the array of probabilities, one can use the setprobabilities message or simply a list. One can query the contents of the variables probabilities, choices, and sum variables, which are sent out the right outlet. The message bang makes a probabilistic choice based on the specified probabilities, and sends the choice (some number from 0 to choices-1) out the left outlet. Note that this is nearly identical to the probabilistic choice capabilities of the table object. It’s shown here as a JavaScript to demonstrate the calculation explicitly.
Tap to set tempo
Instead of the user entering a tempo value by hand, it’s possible to have the computer measure the tempo at which the user is tapping the beat. Do do that, you simply need to measure the time difference between two events (taps).
In this example, I use the ‘t’ key of the computer keyboard (t for tempo, or for tap) to set the tempo attribute of the transport. The timer object measures the time between a bang in its left inlet and a bang in its right inlet. Note that, because of the right-to-eft message-order rules of Max, a bang to both inlets of timer coming from the same outlet of another object will first go to timer‘s right inlet, sending out the time since the previous bang in the left inlet, and only then will it go to timer‘s left inlet to serve as the starting event for the next interval to be timed. Thus each bang message triggered by the ‘t’ key will serve as both the ending event for one time interval measurement and the starting event for the next time interval measurement.
I use a split object to pay attention only to time intervals that would yield a reasonable tempo. I determined that metronomic tempos between 30 and 300 provides an ample range of possibilities. A tempo of 300 bpm implies a beat interval of 200 ms, and a tempo of 30 bpm implies a beat interval of 2000 ms. This also serves the crucial function of filtering out (ignoring) extremely short values that might result from the user inadvertently double-tapping the ‘t’ key, and it filters out the extremely long time intervals that would be measured when the user first taps after not having tapped for a long time. The millisecond time interval between taps is then divided into 60,000 (the number of milliseconds in a minute) to calculate the tempo in terms of beats per minute. (The object !/ means “divide into”, as opposed to / which means “divide by”.) That bpm value is then used as the argument in a tempo message to transport to set the tempo of the global transport in Max. (You can probably imagine how this tap-tempo functionality could be used in conjunction with the metronome demonstrated in the previous example.)
This tap tempo patch allows the user to set the tempo as quickly as possible, with just two taps. There are a couple potential downsides of this quickness, however. One is that the tempo leaps immediately to a new rate with each tap, which could possibly result in some jarring changes. The other is that the user must tap at precisely the right tempo on the first try, or else must keep re-tapping till the right tempo is achieved. A possible method of addressing those potential problems might be to take the average of a few successive taps, thus leading to a slightly more gradual (but still pretty efficient) change to a new tempo. That approach is demonstrated in a tap tempo example from a previous class.
Metronome using General MIDI sounds
When you’re trying to synchronize musical events to a timeline, it’s sometimes useful to have a metronome that tells you where the computer thinks the beat is. The metronome makes a percussive sound on each beat, and ideally makes a unique sound on the first beat of each measure. Most DAW and MIDI sequencing programs have such a feature. This example patch demonstrates a way to implement a transport-synchronized metronome using MIDI messages to trigger percussive clave sounds in a synthesizer.
A computer metronome could trigger any sort of sound: MIDI notes, percussion sounds, recorded samples, synthesized beeps, etc. In this example, I’ve chosen to use two specific MIDI notes, key numbers 75 and 76 on MIDI channel 10 which, according to the General MIDI standard, plays the sounds of Claves and High Wood Block. Those sounds should be roughly the same on any GM-compliant synthesizer, including the synthesizers built into the Mac OS and Windows OS.
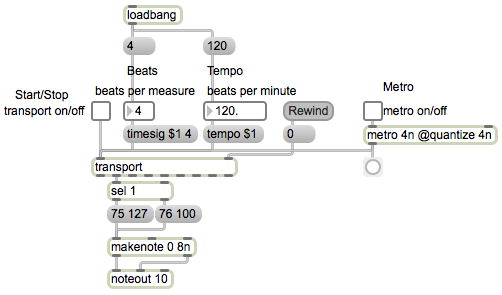
The “global transport” in Max is a timekeeper that’s separate from, but linked to, the main Max scheduler of events. It governs the behavior of timing objects that use tempo-relative timing syntax (note values, bars.beat.units notation, or ticks). The transport object provides an interface within a Max patch to communicate with the global transport. The transport object can be used to control the global transport timekeeper, such as by setting its current time position, setting its tempo, setting its time signature, and starting or stopping it. The transport object can also be queried for that information; a bang in the inlet of transport will send that status info out its outlets.
This example uses both the ‘setting’ and ‘getting’ capabilities of the transport object. The metro object in this patch is initialized with a timing interval of 4n, meaning that when it’s turned on it will send out a bang every quarter note (which, at the default tempo of 120, will be every 500 ms). It also has its quantize attribute set to 4n, which means that its output will be snapped precisely to the quarter note timepoints (the beats) of the global transport. Because the metro interval is states as a tempo-relative timing value (4n), this metro will only run when the global transport is turned on. The textbutton labeled Rewind triggers a 0 message to the right inlet of transport, which resets the global transport to the time position of 0 ticks. The messages 1 and 0 from the toggle labeled Start/Stop turn the transport on or off. In this example, I’ve provided separate toggle switches for turning the global transport on and off and for turning the metro on and off, because in a more elaborate complete program the metronome controls and the transport controls would probably be encapsulated as separate parts of the program. (The user should be able to start and stop the transport in one place, and should be able to turn on or off the option of hearing the metronome in another place.)
Each time the metro sends out a bang, at moments that will necessarily be synchronized with the beats of the global transport, it queries the transport object to find out which beat of the measure it is. If it’s the first beat of the measure, it plays the Claves sound with a dynamic of fortissimo (velocity 127); if it’s any other beat of the measure, it plays the High Wood Block sound with a more moderate forte dynamic (velocity 100). Note that the note durations are set at 8n in the makenote object, to ensure that each MIDI note will be turned off after half a beat’s time.
Using MIDI pitchbend data in MSP
This Max patch demonstrates the arithmetic process of converting a MIDI pitchbend message into a factor that can be used to scale the fundamental frequency of a synthesized tone or the playback rate of a prerecorded sample in MSP.
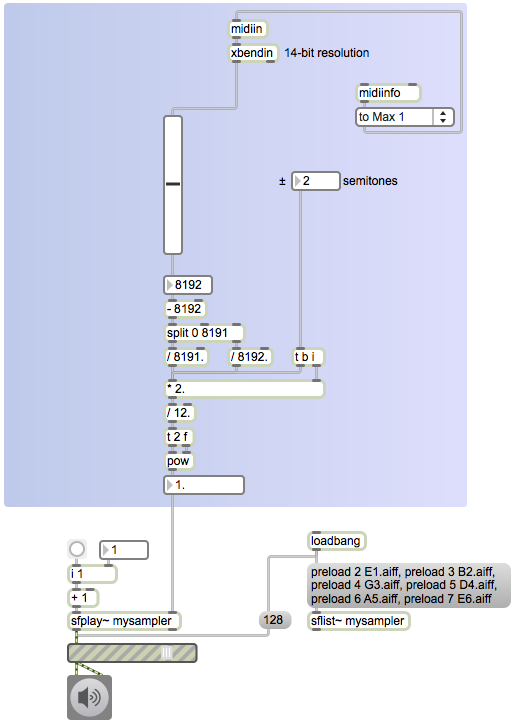
The bendin object uses only the most significant byte (MSB) of the pitchbend message and outputs it as a value from 0 to 127. To get the full 14-bit resolution of an incoming message, one needs to use the midiin object to get the raw MIDI bytes, and then use the xbendin object to recognize pitchbend messages in the data stream, parse those messages, and combine the two data bytes into a single 14-bit value from 0 to 16,383.
A pitchbend value of 8192 (or of 64 if one is considering only the MSB) is considered the central value meaning no change in pitch. But it’s not literally exactly in the center of the range from 0 to 16,383, so in order to map the range 0-16,383 into the range -1 to +1 with 8192 in the center with a value of 0, one needs to treat the values below 8192 differently from the values above 8192. We do this by subtracting 8192 from the value so that the values now occupy the range -8192 to 8191, and then splitting the pitchbend values into two ranges and scaling the negative numbers by 1/8192 and the nonnegative numbers by 1/8191.
Once the values have been mapped into the range -1 to 1, they’re multiplied by the range of semitones desired (a range of ± 2 semitones is the norm). That number is then divided by 12 (the number of equal-tempered semitones in an octave) and that result is used as the exponent of 2 to get the frequency-scaling factor—the value by which we multiply the base frequency of the tone or the playback rate of the sample.
For this patch to work correctly, you must download the six guitar string samples and save the decompressed sound files in the same directory as you save this Max patch.
In this example, we use the frequency-scaling factor to alter the playback rate of a prerecorded note. The sfplay~ object accesses a set of six preloaded sound cues, numbered 2 through 7. Each sound is a single guitar note, played at its original recorded rate. Since a playback rate of 1 gives the original pitch of the note, we can use the scaling factor directly to determine the desired playback rate for the “bent” note.
There are a few other things in this Max patch that bear explanation. Although they’re hidden from view, there are some objects in the patch that are included to make the slider object return quickly to its centered position the way that a real springloaded pitchbend wheel would do. On the left side of the patch there’s a demonstration of the same technique using the 7-bit pitchbend value from a bendin object. The right side of the patch demonstrates that an xbendin2 object will provide the two data bytes of each pitchbend message as two separate 7-bit values, and the patch demonstrates explicitly the bit-shifting and bit-masking operations that take place internally in the xbendin object to make a single 14-bit value.
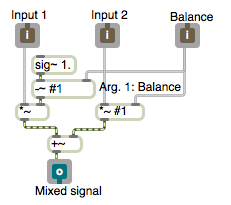
Mix two signals (more efficiently)
This demonstrates a linear interpolation formula for achieving a weighted balance of two signals. It has the exact same effect as the previous mixing example, but uses a more efficient formula, requiring one fewer multiplication per sample.
We want a blend (mix) of two sounds, and we specify the balance between the two as a value from 0 to 1, where a balance value of 0 means we get only the first sound, a balance value of 1 means we get only the second sound, and 0.5 means we get an equal mix of the two sounds.
The way we calculate this is
y[n] = x1[n]+balance(x2[n]-x1[n])
where x1 and x2 are the two signal values and balance is the weighting value described above.
The two audio signals come in the first two inlets, and the balance value comes in the right inlet. The argument #1 will be replaced by whatever is typed in as the object’s first argument when it’s created in the parent patch. This patch subtracts the sound coming in the first inlet from the sound coming in the second inlet, multiplies the result by balance and adds that result to the first sound.
A linear signal from 0 to 1 or from 1 to 0 coming in the right inlet will make a smooth linear crossfade between the two audio signals.
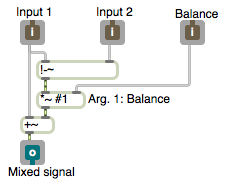
Mix two signals
This demonstrates a linear interpolation algorithm used for achieving a weighted balance of two signals.
Suppose we want a blend (mix) of two sounds, and we would like to be able to specify the balance between the two as a value from 0 to 1, where a balance value of 0 means we get only the first sound, a balance value of 1 means we get only the second sound, and 0.5 means we get an equal mix of the two sounds.
One way to calculate this is
y[n] = x2[n](balance)+x1[n](1-balance)
where x1 and x2 are the two signal values and balance is the weighting value described above.
In this MSP patch (abstraction), the two audio signals come in the first two inlets, and the balance value comes in the right inlet. Note the use of the argument #1, which will be replaced by whatever is typed in as the object’s first argument when it’s created in the parent patch. That allows the programmer to specify an initial balance value when using this abstraction. If the programmer doesn’t type in any argument, the #1 is replaced by 0, by default. The sig~ object provides a constant signal value. So this patch multiplies the sound coming in the first inlet by 1-balance, and it multiplies the sound coming in the second inlet by balance, then adds the two.
If, in the parent patch, the signal in the right inlet is a line~ object going from 0 to 1, the effect will be a linear crossfade between the sound in the first inlet and the sound in the second inlet.
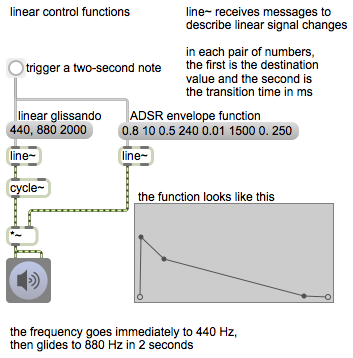
Linear control function
The line~ object generates a signal that interpolates linearly from its current value to a new destination value in a specified amount of time. It receives messages specifying a new value and the amount of time (in milliseconds) in which to get there. If it receives only a single number in its left inlet, it goes to that new value immediately.
We don’t listen to this signal directly (it’s not repetitive, so it’s not audible) but we perceive its effect when it’s used as a control function to change some parameter of a sound-generating algorithm.
Note that a comma (,) in a message box enables you to trigger a series of messages by a single event. In effect, the comma means “End this message and follow it immediately by the next message.” So the message ‘440, 880 2000’ is actually two messages, ‘int 440’ and ‘list 880 2000’. It causes the linear signal to leap immediately to 440 and then transition linearly to 880 in 2000 milliseconds.
When the button is clicked, it triggers messages to both line~ objects. Over the course of 2 seconds, the amplitude is shaped by an ADSR envelope function, and the frequency sweeps from 440 Hz to 880 Hz, resulting in a 2-second note that glides from 440 Hz (the pitch A) to 880 Hz (the A above it).
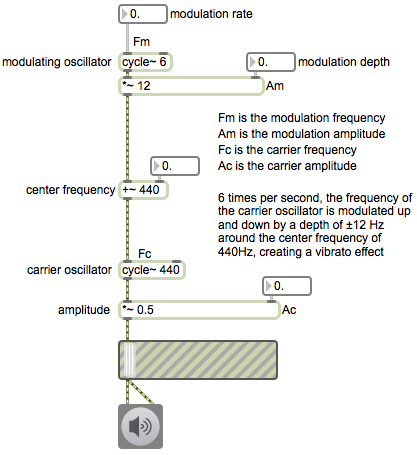
Vibrato
A low-frequency oscillator (LFO) is used here to modulate the frequency of an audio rate oscillator. We don’t hear the LFO directly, but we perceive the shape of its modulating effect on the frequency of the oscillator we do hear.
Print values of a sinusoid
public class PrintWavetable {
// print out values for one cycle of a cosine wave
static final double TWOPI = Math.PI*2.;
public static void main(String[] args) {
int L = 64; // table length
double A = 1.; // amplitude
double phi = 0.; // phase offset
double f = 1.; // frequency
double value; // value of each calculated sample
for (int n=0; n<L; n++) {
value = A*Math.cos(TWOPI*(f*n/L+phi));
System.out.println(value);
}
}
}