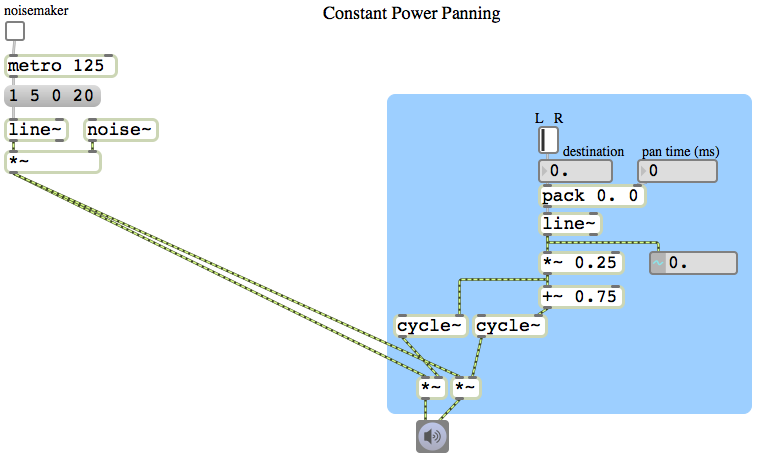
In the previous example we used the square root of the desired intensity for each speaker to calculate the amplitude of each speaker. However, square root calculations are somewhat computationally intensive, and it would be nice if we could somehow avoid having to perform two such calculations for every single audio sample. As it happens, the sum of the squares of sine and cosine functions also equals 1. So, instead of using the square roots of numbers from 0 to 1 (and their complements) to calculate the amplitude for each speaker, we can just look up the sine and cosine as an angle goes from 0 to π/2 (the first quarter of the cosine and sine functions).

In this patch, therefore, we scale the panning value down to a range from 0 to 0.25 and we use that as the phase offset in a 0 Hz cycle~ object. As the panning value moves from 0 to 1, the left speaker’s amplitude is looked up in the first quarter of a cosine function and the right speaker’s amplitude is looked up in the first quarter of a sine function (by adding an additional 0.75 to the scaled phase offset). The resulting effect is just the same as if we performed the square root calculation, but is less computationally expensive.

In most cases this is the preferred method of constant-power intensity panning between stereo speakers. It’s so generally useful that it’s worthwhile to implement it and save it as an abstraction, for use as a subpatch in any MSP program for which stereo panning is required. An abstraction version of this method is demonstrated in Example 43 from the 2009 class.