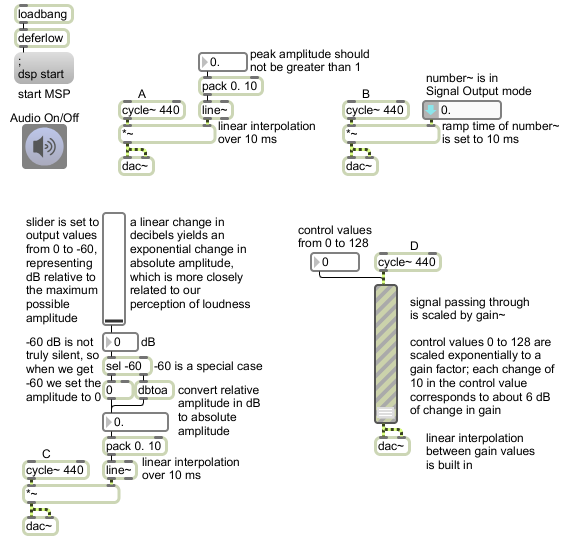
As explained in MSP Tutorial 2, in order to avoid creating clicks in audio when you change the amplitude, you need to interpolate smoothly from one gain value to another. Example A in this patch shows how to use the line~ object to do that. The gain value from the number box is combined with a transition time in the pack object (10 ms in this case) and the two numbers are sent as a list to line~. The line~ object interpolates to the new value sample-by-sample over the designated transition time (i.e. over the course of about 441 samples) to get to the destination gain value smoothly. Example B does exactly the same thing, but uses a single object, number~, to accomplish the same functionality as was achieved with number box, pack, and line~ in Example A. Note that the number~ object is in Signal Output mode (with the downward arrow on the left of the object), which enables it to function like a float number box and send out its value in the form of a signal (with a designated interpolation time).

To create a fade-in or fade-out that sounds linear to us perceptually, we actually have to do a fade that is exponential. Doing a linear fade in the decibel scale and then converting that value to an actual amplitude (gain) value is a good way to get a fade that sounds “right” (smooth and perceptually linear). The 16 bits of CD-quality digital audio theoretically provide up to 96 decibels of dynamic range, but in most real-world listening situations we probably only have 60 to 80 decibels of usable dynamic range above the ambient noise floor. Example C permits control of the amplitude of the signal in a range from 0 dB (full volume) down to -59 dB (very soft), and if the user chooses -60 dB with the slider (very soft but still not truly silent), we treat that as a special case by looking for it with the select -60 object, and turn the gain completely to 0 at that point.

The gain~ object in Example D combines the functionality of slider, exponential scaling (as with the scale object), line~, and *~. It’s handy in that regard, because it takes care of lots of the math for you, but because its inner mathematics are not very intuitive to most users, you might find you have more precise control by building amplitude controls yourself in one of the ways shown in Examples A, B, and C.

For some very similar examples, with slightly different explanation, see linear interpolation of audio.