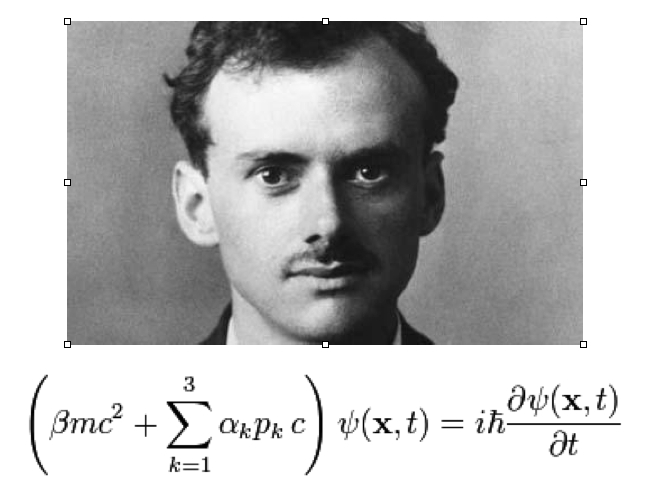This is to elaborate the interactions of the Higgs and the Weak Bosons with the quarks and electrons, specified by the concept of a weak isospin analogous to ordinary spin angular momentum. This article covers the theory of spin angular momentum.
Quantum mechanics shows that the angular momentum of the smallest pieces of matter is not continuous, but is quantized in units of hbar = h/2π, where hbar is a very small number and h is Planck’s constant. In regular quantum mechanics for massive atoms at rest, the orbital angular momentum L of an electrons in an atom is quantized in units of hbar, and can be L = n*hbar, where n is an integer, n = 0, 1, 2, etc. The angular momentum component can only be determined about a one specific axis or direction at a time, and this is usually taken as the z axis or the 3 direction. The angular momentum component along the z axis, m = Lz, runs through integers from -L to +L. For L = 0, m = 0. For L = 1, m = 1, 0, or -1. For L = 2, m = 2, 1, 0, -1, or -2. Electromagnetic transitions between different states of the electron conserve Lz when one includes the angular momentum projection of the emitted photon, which is has orbital angular momentum coupled to its spin of 1.
When considering the fundamental particles, relativity must be added to quantum mechanics. This results in allowing the values of angular momentum of the fundamental particles, called their spin, to include at S = 1/2 hbar, and include 3/2 hbar, etc., along with the integers S = n * hbar. For a spin 1/2 particles, two values of its spin along the z axis are allowed, Sz = +1/2 hbar, and Sz = -1/2 hbar. For a massive spin = 1 (S = 1 hbar), just like for orbital angular momentum, Sz = +1, 0, and -1 are allowed. But for a massless spin 1 particle like the photon, only Sz = +1 and -1 along its direction of motion are allowed. Spin 1/2 particles are called Fermions and obey Fermi-Dirac statistics and the Pauli Exclusion Principle where two cannot exist in the same state, which builds up the atomic orbitals. The integer spin particles are called Bosons, and obey Bose-Einstein statistics, where many can exist in the same state.
The spin 1/2 Fermions were actually discovered theoretically when Paul Dirac formulated a relativistic quantum mechanical equation of motion analogous to the Schrodinger equation.
Another outcome of Dirac’s Equation was the discovery of negative energy states with the same mass but a charge of opposite sign. This was the discovery of anti-particles, such as the positively charged positron is the anti-particle of the negatively charged electron.
We should add here that in a system with no preferred axis or direction, that is with no outside forces or interactions that have an axis or direction, then the system is invariant or unchanged by rotations. Rotational invariance leads to the conservation of angular momentum. This is an example of the Noether theorem formulated by Emmy Noether that associates a conserved quantity with a symmetry. Emmy Noether (1882-1935) was described as the most important woman in the history of mathematics.
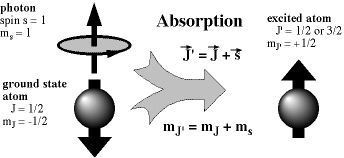
An example of a photon interacting with the magnetic moment of a spin 1/2 proton or nucleus in a magnetic field and being absorbed by it to flip its spin to a higher energy state is the basis of nuclear magnetic resonance, now called magnetic resonance imaging:
A moving spin 1/2 particle’s spin can be referred to as along its direction of motion as positive helicity, or right-handed. If the particle’s spin is opposite its direction of motion, it can be referred to as negative helicity, or left-handed.
Photons, which are massless spin 1 particles, can only have their spin along or opposite their direction of motion, and are then referred to also as right circularly polarized or left circularly polarized, respectively.