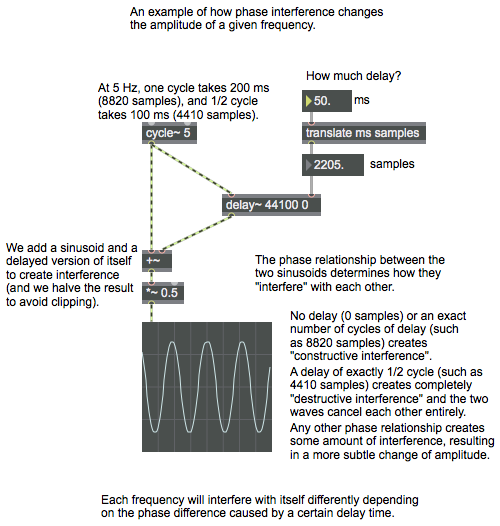
A sinusoid added to a delayed version of itself will result in a sinusoid of the same frequency but with its amplitude altered. The amount of amplitude change will depend on the phase relationship between the original sinusoid and its delayed copy. The two sinusoids will “interfere” with each other either constructively (reinforcing each other) or destructively (tending to cancel each other). For example, two sinusoids that are out of phase by exactly one-half cycle will theoretically completely cancel each other, because one is effectively a flipped version of the other around the x axis (i.e., around 0 on the y axis).
The amount of phase difference caused by delay depends on the delay time and the frequency of the sinusoid in question. Because every complex sound is composed of energy at multiple frequencies, in effect, it’s the sum of many sinusoids. Mixing any sound with a slightly delayed copy of itself will therefore alter the amplitude of each of the component frequencies of the sound, in varying amounts depending on the delay time and the frequencies involved.
This patch allows you to experiment with delay applied to a single sinusoid, to notice the interference effect. Bear in mind that this sort of effect occurs on every frequency component of any sound treated in this way.
In the example, we view a 5 Hz sinusoid. It’s not audible, of course, but because of its low frequency it’s easy to view in a scope~ object, and it’s easy to calculate the period of one cycle. (The period is the inverse of the frequency, so the period is 1/5 second, which is to say 200 milliseconds.) And with a sample rate of 44,100 Hz, it’s pretty easy to calculate how many samples are used for one cycle of the waveform (8820 samples) and how many samples correspond to one-half cycle of the waveform (4410 samples).