Author Archives: mgalvao

Rhythmic delays in time with a musical tempo

Image

The tempo-relative timing capabilities in Max can be used to synchronize MSP processing in time with a musical beat. In this example, timings of delays are specified in tempo-relative time units so that they remain rhythmically correct for any tempo.

Click on the button above the click~ and you will hear a click followed by four rhythmically delayed versions of the click (with diminishing amplitudes). The timings of the delays have been set to a dotted eighth note, a dotted quarter note, a double-dotted quarter note, and a half-note-plus-a-sixteenth. The tapout~ object does not interpret tempo-relative time syntax on its own, so we use the translate object to convert time musical units such as 8nd or bars.beats.units such as 0.1.360 into milliseconds.

Now try changing the tempo of the transport to some other tempo such as 96 bpm, and then trigger the click again. Notice how the rate of the rhythm has changed commensurate with the change in the global tempo. Finally, start the transport, which will also start the metro, which will begin playing a different sound every quarter note. Since the delays are all set to happen on sixteenth note pulses somewhere between the quarter notes, you will hear a composite rhythm that is more complex than is actually being played by the metro. If you change the tempo, the delays will stay in the same rhythmic relationship to the quarter-note beat.

Windowing an audio signal

Image

In signal processing, a “window” is a function (shape) that is nonzero for some period of time, and zero before and after that period. When multiplied by another signal, it produces an output of 0 except during the nonzero portion of the window, when it exposes the other signal. The simplest example is a rectangular window, which is 0, then briefly is 1, then reverts to 0. The windowed signal will be audible only when it is being multiplied by 1 — i.e., during the time when the rectangular windowing occurs. Many other window shapes are possible: trapezoidal, triangular, a “sine” window (the first half of a sine wave), etc.

Windowing is most often used in spectral analysis, to view a short time segment of a longer signal and analyze its frequency content. Windows are also used to create short sound segments of a few milliseconds’ duration called “grains”, which can be combined into granular sound clouds for unique sorts of synthesis. In general, one can think of any finite sound that has a starting point and a stopping point as being a windowed segment in time. For example, a cycle~ object is always producing a signal, but we can window it with a *~ object, keeping its amplitude at 0 except when we want to hear it. However, a rectangular window — suddenly switching from 0 to 1 and then back from 1 to 0 — will usually create a click, so other window shapes are usually more desirable.

This patch shows several ways to create a window function in MSP. To read through the function, you need some sort of linear signal such as line~, phasor~, count~, or the right outlet of groove~. The MSP objectstrapezoid~ and triangle can convert a linear 0-to-1 signal into various sorts of trapezoidal or triangular functions. You can also use a math expression to calculate some other function arithmetically; you can either do that on the fly or, more economically, do it in advance, store the result in a memory buffer, then read through the buffer whenever you need that window shape. That last method is what’s being done with the buffer~, peek~, and play~objects.

In the top left part of the patch, we see some ways to obtain useful constants for mathematical computations. For example, pi and 2pi are numbers that are often needed for computing a cyclic waveform (or a part of one). Once you know the constant value you need, you can plug it into your own math expression. The sampstoms~ object is useful for figuring out how many milliseconds correspond to a certain number of audio samples. (And the reverse calculation can be made using its counterpart mstosamps~.) In this case, we learn that 512 samples at a sampling rate of 44,1000 Hz is equal to 11.61 milliseconds, so we create a buffer~ of exactly that length. Then we use uzi, expr, and peek~ to quickly fill that buffer with 512 samples describing half of a sine wave, which will be our window shape. (Double-click on the buffer~ to see its contents.) The formula for another common window shape, known as a Hann window, is also shown just below that.

Then, you can play a sound file with sfplay~, choose one of the three window functions with the selector~ (the sine window is initially chosen by default), and trigger a window to occur by clicking on the button at the top of the patch.

This sort of windowing technique is useful for shaping the amplitude envelope of sampled sounds or any other audio signals, in order to avoid clicks and to create the sort of attack and release characteristics you want for a sound, whether it be a short grain or a longer excerpt.

Mixing multiple audio processes

Image

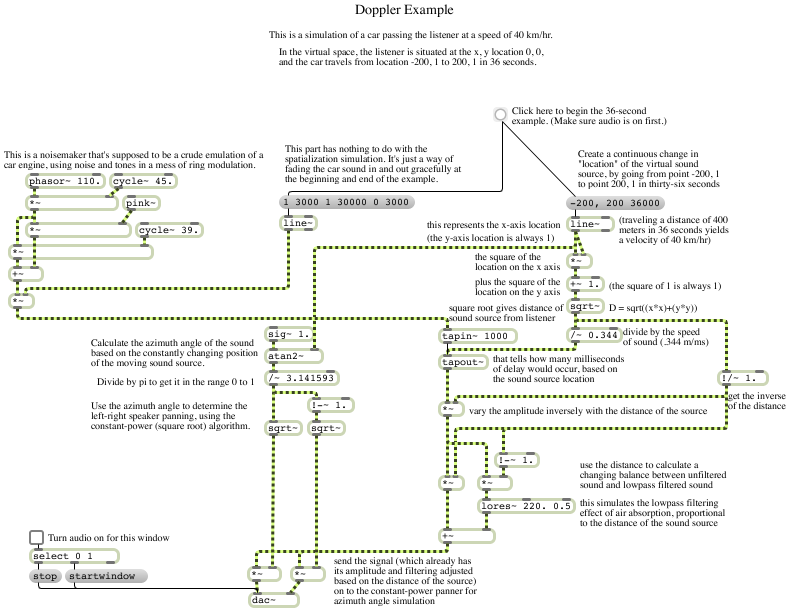
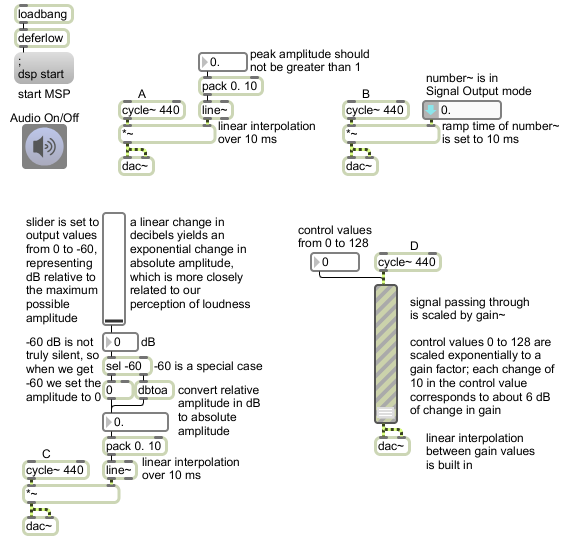
pinger: a beeping test sound.

This patch is designed to be used as an abstraction (subpatch) in the next example. In order for the next example to work, you should download this example and save it with the filename “pinger.maxpat” somewhere in the Max file search path.

Its purpose is just to generate a recognizable sound. It emits very short sinusoidal beeps of a specified frequency, at a rate of a specified number of beeps per second, panning back and forth from left to right a specified number of times per second. These three parameters — tone frequency, note rate, and panning rate — are specified as arguments 1, 2, and 3 in the parent patch.

Because this abstraction was designed just to be used as a test tone in a particular example, it just uses the simple #1, #2, and #3 arguments as a way of providing the parameter values (as unchangeable constants typed in the parent patch). To make a more versatile program, one could also provide inlets to receive variable values, and could use patcherargs to provide useful default initial values. Compare, for example, the lmap abstraction.

 

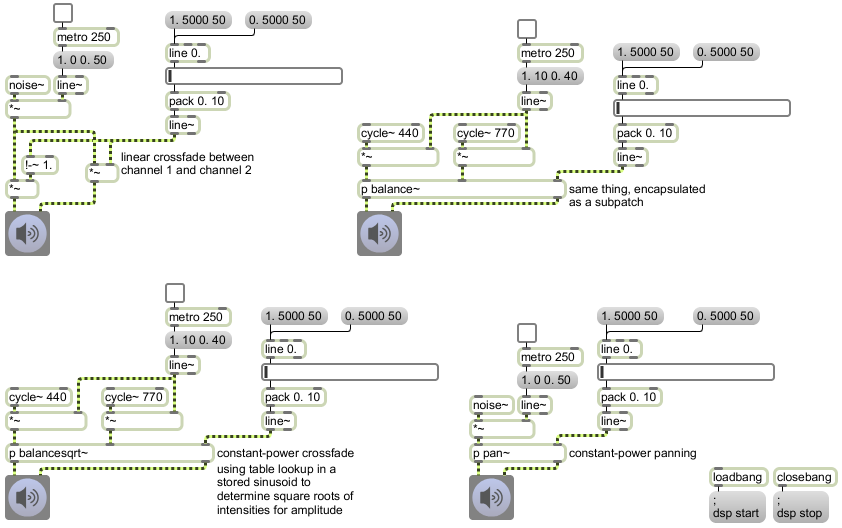
Mixing multiple audio processes

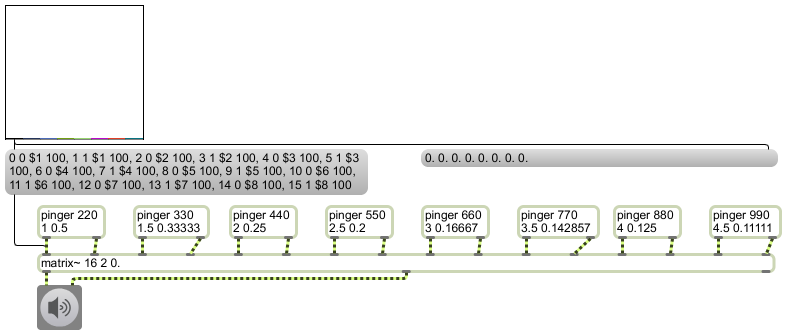
For this example to work correctly you will need to first download the pinger abstraction above and save it with the filename “pinger.maxpat” somewhere in the Max file search path.

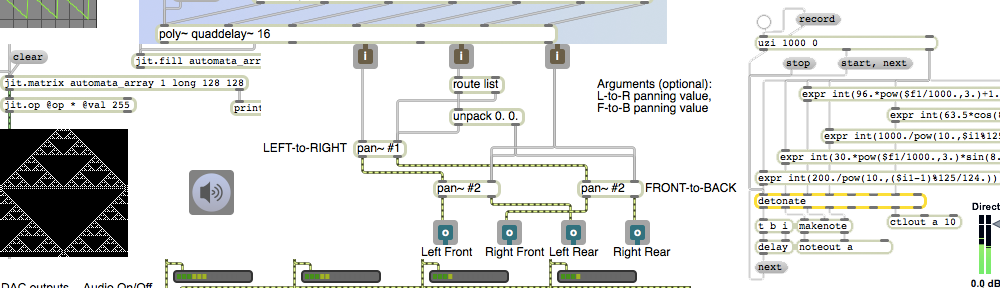
This example shows the use of the matrix~ object to mix together different sounds. Think of matrix~ as an audio mixer/router (a kind of combination of mixer and patch bay). The first two arguments specify the number of inlets and outlets, and the third argument specifies the default gain factor for each inlet-outlet connection.

Inlets and outlets of matrix~ are numbered starting from 0. So, in this example there are 16 inlets (numbered 0 to 15) and 2 outlets (numbered 0 to 1). (There’s always an extra outlet on the right, from which informational messages are sometimes sent.)

Messages to the left inlet of matrix~ generally take the form of a four-item list to specify an inlet, an outlet to be connected that inlet, a gain factor (multiplier) for sounds that will flow from that inlet to that outlet, and a ramp time to transition smoothly to that gain factor (to avoid clicks). You can send as many such messages as you’d like, to specify as many connections as you want.

In this example we have connected eight stereo pinger objects to the 16 inlets of matrix~, and we will mix them all together for a single stereo output. The pinger objects are just stand-ins for what could potentially be any eight different audio processes you might want to mix together. The arguments to pinger specify frequency of the beep tone, the number of notes per second, and the rate of panning. For example, the first pinger plays a 220 Hz tone 1 time per second (i.e., at a rate of 1 Hz), panning left to right once every two seconds (i.e. at a rate of 0.5 Hz). The next pinger plays a 330 Hz tone at a rate of 1.5 notes per second (i.e. once every 666.6667 milliseconds), panning left to right once every three seconds (i.e., at a rate of 0.33333 Hz), and so on. The result is 8 tones (harmonics 2 through 9 of the fundamental frequency of 110 Hz) at 8 different harmonically-related rhythmic rates, panning back and forth at 8 different harmonically-related rhythmic rates.

With matrix~ you can mix these eight tones in any proportion you want, but how can you easily control all eight amplitudes at once? If you had a MIDI fader box, you could map the eight control values from the faders to the gain factors of the various connections. In the absence of such a fader box, we use the multislider object, set to have 8 sliders, that sends out a list of eight values from 0. to 1. corresponding to the vertical position of each slider as drawn with the mouse. So, by clicking and/or dragging with the mouse on the multislider you can set eight level values for use by matrix~. That list of eight values is sent to the right inlet of the right message box so we can see the values, and it’s also sent to the left inlet of the left message box where the values are used in sixteen different connection messages to matrix~.

Take a moment to examine and understand those messages. The first message says “connect the first inlet [inlet 0] to the first outlet [outlet 0] multiplied by a gain factor [the value of the first slider] with a transition time of 100 milliseconds, and so on. Each pair of messages controls a pair of inlets corresponding to one of the pingers, and sets the gain with which that pinger will go to the output.

Turn on audio audio by clicking on the ezdac~, then try out the patch by moving the sliders in the multislider. Note that when you add together eight different audio processes, each playing at full volume, you need to be careful about the sum of all your gain factors. A more elaborate patch would, at the least, provide a volume control for the final summed signal. Even more desirably, perhaps, the final volume control could be constantly controlled automatically, proportionally to the sum of the slider values, to prevent clipping of the output signal.

Using gate to route messages

Image

You can assign input data to have a different function at different times, simply by sending it to different parts of your program. For example, if you have a control device such as a MIDI keyboard or other MIDI controller with a limited number of keys, buttons, knobs, or faders, you can assign one control element to be the mode selector that changes the functionality of all the other elements. This program demonstrates one easy way to direct incoming MIDI note data to different destinations (where the data could have a different effect) using the gate object.

The argument to gate specifies how many outlets it should have. Messages that come in the right inlet are passed out the outlet specified by the most recent number received in the left inlet. (An optional second argument can specify which outlet should be open initially.) The outlets are numbered starting with 1. If the most recently received number in the left inlet is 0, or no open outlet has been specified, all outlets are closed.

In this patch, you can specify the open outlet via the number box, or by typing a number on the computer keyboard. Since the keys 0 to 9 on the keyboard have the ASCII values 48-57, it’s easy to turn the ASCII values into the numbers 0 to 9 just by subtracting 48 from them. In the upper-left portion of the patch, we get the ASCII values with the key object, look only for ASCII values in the range 48 to 56 (keys 0 to 8), and subtract 48.

In the upper-right portion of the patch, we get MIDI note data (pitches and velocities) with the notein object, pass the pitches and velocities through a flush object, and pack them together as a two-item list with the pack object so that they can go into the right inlet of gate as a single message (thus keeping the pitch and velocity linked together).

Because the data that we’re redirecting with gate is MIDI note data it’s important that we not switch outlets while a MIDI note is being held, because that would likely result in a stuck note (a note-on message without a corresponding note-off message) somewhere in the program. For that reason, each time that we detect a change in the specified outlet number (with the change object), we first send a bang to the left inlet of flush, which causes it to sent out note-off messages for each held note-on, before we pass the new outlet number to the left inlet of gate. That ensures that the note-off messages go out the previously open outlet before we switch to a new outlet for subsequent notes. (This practice of making sure you neatly close down one process when switching to another is a good habit to develop in your programming.)

Line segment control functions

Image

The line~ object is intended for use as a control signal for audio. You don’t listen to line~ directly, but it’s very effective as a controller/modifier/modulator of other signals. A pair of numbers (i.e. a two-item space-separated list of numbers) tells line~ a destination value and a time (in milliseconds) to get to that value. For example, the message 0.99 100 tells line~ to change its signal value from whatever it currently is to 0.99, moving linearly sample-by-sample toward 0.99 over the course of 100 milliseconds, calculating the intermediate signal value for each sample along the way. The result is a smoothly changing signal.

You can also send line~ a list that has more than two numbers. Every two numbers in the list are viewed as a “destination value / transition time” pair. The output of line~ follows the instructions of the first pair of numbers, then immediately follows the second pair, and so on. Thus, one can create a variety of control function shapes by specifying the destination value and transition time for each line segment.

In this patch, try clicking on the message box that says “example of a guitar-like pluck”. The amplitude of the sound goes to full (0.99) in 1 millisecond, dies by -12 dB (to 0.25) in the next 99 milliseconds, dies another -14 dB (to 0.05) in the next 900 milliseconds, and then fades entirely to 0 in 3000 ms. The result is a 4-second note with roughly the amplitude envelope of a plucked string.

The message box just below that, labeled “fade-in, stay, fade-out”, describes a very slow fade-in and fade-out. It goes to an amplitude of 0.5 in 2 seconds, stays there for 3 seconds, then fades to 0 in 5 seconds. The same sort of line segment function can also be used to control other aspects of a sound. The message box labeled “line segment control of frequency” specifies frequency values (to send a constantly changing frequency to cycle~) instead of amplitude values. It causes the frequency of the message box to jump immediately to 220 Hz, glide to 660 Hz in 3 seconds, shoot quickly down to 110 Hz in 5 milliseconds, then glide up to 440 Hz in about 7 seconds.

The function object allows you to draw a line segment function by clicking at the desired breakpoints. You can set the domain of that function (the total time of of the x axis) in the object’s Inspector or with a setdomainmessage. In this example, we have set the function‘s domain to 10 seconds (10,000 ms). When the object receives a bang, it sends out its second outlet a list of destination value / transition time pairs that are designed to go to aline~ object, and that correspond to the shape of the drawn function. So, in this example we use one button to trigger the function to send a 10-second line segment function to the line~ that controls amplitude at the same time as we trigger the message box to send a 10-second function to the line~ that controls the frequency of the cycle~. The result is continuous modulation of the oscillator’s frequency and its amplitude.

For more on the use of line segment control functions, see the chapters on the Algorithmic Composition blog, titled “Line-segment control function” and “Control function as a recognizable shape“.

It’s worth pointing out that the cycle~ object in this example uses 512 samples of a stored waveform in a buffer~ instead of its default cosine waveform. By giving a cycle~ object the same name as a buffer~, you instruct it to look at 512 samples of that buffer~ for its wavetable. The waveform being used in this example is one cycle of an electric guitar chord.

Audio amplitude control

Image

As explained in MSP Tutorial 2, in order to avoid creating clicks in audio when you change the amplitude, you need to interpolate smoothly from one gain value to another. Example A in this patch shows how to use the line~ object to do that. The gain value from the number box is combined with a transition time in the pack object (10 ms in this case) and the two numbers are sent as a list to line~. The line~ object interpolates to the new value sample-by-sample over the designated transition time (i.e. over the course of about 441 samples) to get to the destination gain value smoothly. Example B does exactly the same thing, but uses a single object, number~, to accomplish the same functionality as was achieved with number box, pack, and line~ in Example A. Note that the number~ object is in Signal Output mode (with the downward arrow on the left of the object), which enables it to function like a float number box and send out its value in the form of a signal (with a designated interpolation time).

To create a fade-in or fade-out that sounds linear to us perceptually, we actually have to do a fade that is exponential. Doing a linear fade in the decibel scale and then converting that value to an actual amplitude (gain) value is a good way to get a fade that sounds “right” (smooth and perceptually linear). The 16 bits of CD-quality digital audio theoretically provide up to 96 decibels of dynamic range, but in most real-world listening situations we probably only have 60 to 80 decibels of usable dynamic range above the ambient noise floor. Example C permits control of the amplitude of the signal in a range from 0 dB (full volume) down to -59 dB (very soft), and if the user chooses -60 dB with the slider (very soft but still not truly silent), we treat that as a special case by looking for it with the select -60 object, and turn the gain completely to 0 at that point.

The gain~ object in Example D combines the functionality of slider, exponential scaling (as with the scale object), line~, and *~. It’s handy in that regard, because it takes care of lots of the math for you, but because its inner mathematics are not very intuitive to most users, you might find you have more precise control by building amplitude controls yourself in one of the ways shown in Examples A, B, and C.

For some very similar examples, with slightly different explanation, see linear interpolation of audio.

Random note choices

Image

The left part of this example shows the use of the random object to make arbitrary note choices. Every time random receives a bang in its inlet, it sends out a randomly chosen number from 0 to one less than its argument. In this case it chooses one of 61 possible key numbers, sending out a number from 0 to 60. We then use a + object to offset that value by 36 semitones, transposing up three octaves to the range 36 to 96 — cello low C to flute high C. Similarly, we choose one of 8 possible velocities for each note. The random object sends out a number from 0 to 7, which we scale by a factor of 16 and offset by 15, thus yielding 8 possible velocities from 15 to 127. These choices by the random objects are made completely arbitrarily (well, actually by a pseudo-random process that’s too complex for us to detect any pattern), so the music sounds incomprehensible and aimless.

One can make random decisions with a little bit more musical “intelligence” by providing the computer with a little bit of musically biased information. Instead of choosing randomly from all possible notes of the keyboard, one can fill a table with a small number of desirable notes, and then choose randomly from among those. In the middle example, we have filled lookup tables with 16 possible velocity values and 16 possible pitches. Each time we want to play a note, we choose randomly from those tables. The velocities are mostly mezzo-forte, with only one possible forte value and one fortissimo value. Thus, we would expect that most notes would be mezzo-forte, with random accents occurring unpredictably on (on average!) one out of every eight notes. The pitches almost all belong to a Cm7 chord, with the exception of a single D and a single A in the upper register. So, statistically we would expect to hear a Cm7 sonority with an occasional 9th or 13th. There’s no strong sense of melodic organization, because each note choice is made by random with no regard for any previous or future choices, but the limited, biased set of possibilities lends more musical coherence to the results.

In a completely different usage of the table object, you can use table as a probability distribution table, by sending it bang messages instead of index numbers. When table receives a bang, it treats its stored values as relativeprobabilities, and sends out a chosen index number (not the value stored at that index) with a likelihood that corresponds to the stored probability at that index. Double-click on the table objects in the right part of the patch to see the probabilities that are stored there. In the velocity table, you can see that there is a relatively high probability of sending out index numbers 4 or 5, and a much lesser likelihood of sending out index numbers 1 or 7. These output numbers then get multiplied by 16 to make a MIDI velocity value. Thus we would expect to hear mostly mezzo-forte notes (velocities 64 or 80) and only occasional soft or loud notes (velocities 16 or 112). In the pitch table, you can see that the index numbers with the highest probabilities are 0, 4, 7, and 11 respectively, with a very low likelihood of 2, 9, or 12. These values have 60 added them to transposed them to the middle octave of the keyboard. So we would expect to hear a Cmaj7 chord with only a very occasional D or A.

To learn more about the use of table to get weighted distributions of probabilities, read the blog article on “Probability distribution”.