Tag Archives: amplitude

Amplitude envelope with the function object

Image

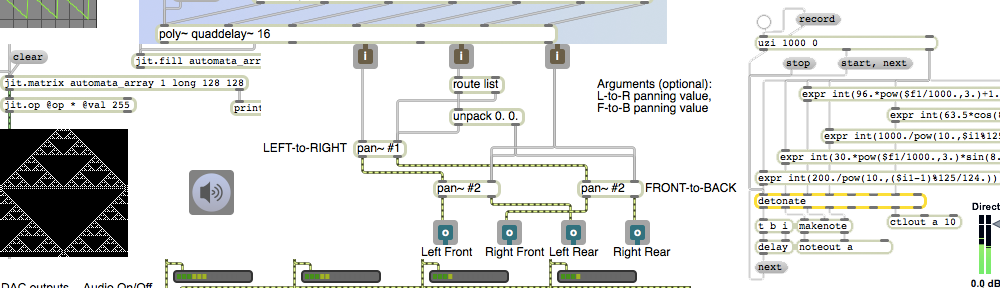
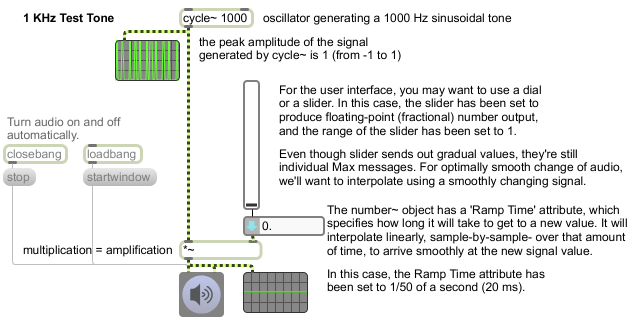
In MSP, each MSP object (each object that has signal input and/or output) is always producing signal as long as audio is turned on. For example, signal generators like cycle~(sinusoidal wave generator) and saw~ (band-limited sawtooth wave generator) are always producing a full-amplitude wave. You control the amplitude of that wave with multiplication, using *~ or some other object that performs a multiplication internally (such as gain~). Multiplication by a value greater than 1 increases the amplitude (amplification), and multiplication by a value between 0 and 1 decreases the amplitude (attenuation). (Multiplication by a negative number has the same sort of effect, while also inverting the signal about the x axis.) Multiplication by 0 completely suppresses the signal (silence). In that last case, the signal generator is still working just as hard, producing its full amplitude signal, but the multiplication by 0 converts every sample to 0.

You can think of every individual sound as being surrounded by silence. You could imagine that, as in MSP, sound is always present, but during the silence its amplitude is 0 (the sound is being multiplied by 0), and when the sound is audible it is being multiplied by 1 or by some other nonzero number. Thus, the sound is audible only when its amplitude is being controlled by a nonzero value — a conceptual “window” is opened on the sound allowing it through — and the rest of the time it’s being multiplied by 0 and the conceptual window is closed. This idea of a “window” — a period of nonzero values surrounded by 0 before and after — is an important concept in digital music and in digital signal processing. A sound that is off (0), then is instantaneously switched on (1), then is later instantaneously turned off again (0) has been windowed with a rectanglar-shaped function. More commonly in music software we use a window shape that is not exactly rectangular, such as a trapezoidal window with tapered ends, to avoid clicks.

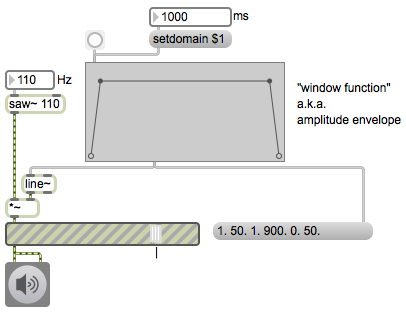
This example demonstrates the use of a function object to create a trapezoidal window signal coming out of the line~ object to control the amplitude of a sawtooth oscillator. Each time function receives a bang, it sends out a list that says, “Go to 1 in 50 milliseconds, stay at 1 for 900 milliseconds, then go to 0 in 50 milliseconds.” The changing values fromline~ are used as the multiplier controlling the amplitude of the oscillator, opening a 1-second window on the sound.

The duration of that window can be changed simply by sending a setdomain message to function. Note that the duration of each segment of the function is time-scaled proportional to the domain specified, so the fade-in and fade-out tapered ends of the function, which are 50 milliseconds initially, would last only 5 milliseconds if the duration of the window were shortened to 100 ms, and would last 500 milliseconds if the total duration (the domain) were set to 10,000 ms.

Using matrix~ for multi-channel audio amplitude control

Image

This example shows how to control the amplitude of multiple signals with the matrix~ object, instead of with line~ and *~ objects. In effect, matrix~ has the linear interpolation and multiplication capabilities of those objects embedded within it.

The matrix~ object can be thought of as a mixer/router of audio signals. The arguments to matrix~ specify the number of audio inlets, the number of audio outlets (there’s always one additional outlet on the right), and the initial gain for the connections of inlets to outlets. Each inlet is potentially connectable to each outlet with a unique gain setting; the gain of the connections is changed by sending messages in the left inlet.

The messages in the left inlet of matrix~ specify an inlet number (numbered starting from 0), an outlet number, a gain factor for scaling the amplitude of that connection, and a ramp time in milliseconds to arrive at that amplitude. You can send as many such messages as needed to establish all the desired connections.

In this example we have a matrix~ with two inlets and one outlet. A full-amplitude sinusoidal audio wave is coming in each inlet, but we don’t hear anything initially because the third argument of the matrix~ has set the initial gain of all connections to 0. When you click on the left message box, it sends two messages meaning, “Connect inlet 0 (the leftmost inlet) to outlet 0 (the leftmost outlet) with a gain factor of 0.5 getting there in 10 seconds, and also connect inlet 1 to outlet 0 with a gain of 0.5 getting there in 10 seconds as well.” When matrix~ receives those two messages, it begins the linear interpolation of those connections to 0.5 gain over 10 seconds. (We chose a gain of 0.5 so that the sum of the signals would not exceed 1.) When you click on the message box on the right, it will set the gain of both of those connections to 0 in 100 milliseconds.

This method of sending a message for each possible connection may seem a bit cumbersome when you’re controlling a matrix with many inputs and outputs, but in fact it’s about the most efficient way to control a large matrix (a virtual patchbay) of possible connections. With some clever message management, you can control or automate a great many constantly-changing connections. You can re-route inlets to outlets as need be, and you can control the amplitude of all the connections.

For some slightly more elaborate examples of the use of matrix~, see the examples called Using matrix~ for audio routing and mixing and Mixing multiple audio processes.

Audio amplitude control

Image

As explained in MSP Tutorial 2, in order to avoid creating clicks in audio when you change the amplitude, you need to interpolate smoothly from one gain value to another. Example A in this patch shows how to use the line~ object to do that. The gain value from the number box is combined with a transition time in the pack object (10 ms in this case) and the two numbers are sent as a list to line~. The line~ object interpolates to the new value sample-by-sample over the designated transition time (i.e. over the course of about 441 samples) to get to the destination gain value smoothly. Example B does exactly the same thing, but uses a single object, number~, to accomplish the same functionality as was achieved with number box, pack, and line~ in Example A. Note that the number~ object is in Signal Output mode (with the downward arrow on the left of the object), which enables it to function like a float number box and send out its value in the form of a signal (with a designated interpolation time).

To create a fade-in or fade-out that sounds linear to us perceptually, we actually have to do a fade that is exponential. Doing a linear fade in the decibel scale and then converting that value to an actual amplitude (gain) value is a good way to get a fade that sounds “right” (smooth and perceptually linear). The 16 bits of CD-quality digital audio theoretically provide up to 96 decibels of dynamic range, but in most real-world listening situations we probably only have 60 to 80 decibels of usable dynamic range above the ambient noise floor. Example C permits control of the amplitude of the signal in a range from 0 dB (full volume) down to -59 dB (very soft), and if the user chooses -60 dB with the slider (very soft but still not truly silent), we treat that as a special case by looking for it with the select -60 object, and turn the gain completely to 0 at that point.

The gain~ object in Example D combines the functionality of slider, exponential scaling (as with the scale object), line~, and *~. It’s handy in that regard, because it takes care of lots of the math for you, but because its inner mathematics are not very intuitive to most users, you might find you have more precise control by building amplitude controls yourself in one of the ways shown in Examples A, B, and C.

For some very similar examples, with slightly different explanation, see linear interpolation of audio.

Adjusting audio amplitude

Image

 

The operation of amplification in audio (turning the volume up or down) corresponds to the mathematical operation of multiplication in your program. If you send a Max message to the *~ object to provide a new multiplier value, the amplitude of the audio signal might change so abruptly as to cause an unwanted click in the sound, as described in MSP Tutorial 2. To avoid such clicks, you need to use a control signal instead, one that interpolates to the new multiplier sample-by-sample over the course of a small amount of time. The number~ object is capable of doing that. It ramps smoothly to a new value over a number of milliseconds that you can specify in theRamp Time attribute in the object’s Inspector. (You can also set the ramp time via the object’s right inlet.)

Linear Mapping of MIDI to Amplitude

Image

 

Data from a MIDI continuous controller (such as a mod wheel or a volume pedal), and/or from a Max slider object, can be used to control the amplitude of an audio signal. First the data is mapped into the appropriate range (e.g., 0 to 1), then it is used as a multiplier for the audio signal.

Note that to be truly correct, the data should go to a line~ object to interpolate sample-by-sample to the new amplitude over a very small amount of time (say, 20-50 ms or so) before going to the *~ objects. That step is omitted from this program just to simplify. You can see an example of this use of line~ in the example from April 5, 2006 called “Simple audio file player”.

Linear mapping can be achieved by a multiplication to resize the range and an addition to offset the range. The zmap object (shown but not used) can do this for you. Linear interpolation over a period of time can be achieved by using the line object for Max messages (as shown in the upper right corner) or the line~ object for audio signals (not shown in this example).

To read more about linear interpolation and linear mapping, see also Dobrian’s blog chapters on linear change and fading my means of interpolation.