Tag Archives: interpolation

Interpolation with the function object

Image

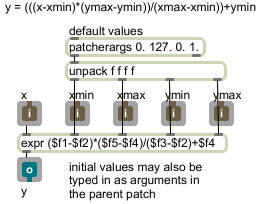
The function object can be used to create line segment functions that control a line~ object, and it can also be used as a lookup table. A number coming in its inlet will be treated as a point on the x axis, and whatever y axis value is shown on the line segment function at that point will be sent out the leftmost outlet. This example patch demonstrates that use of function.

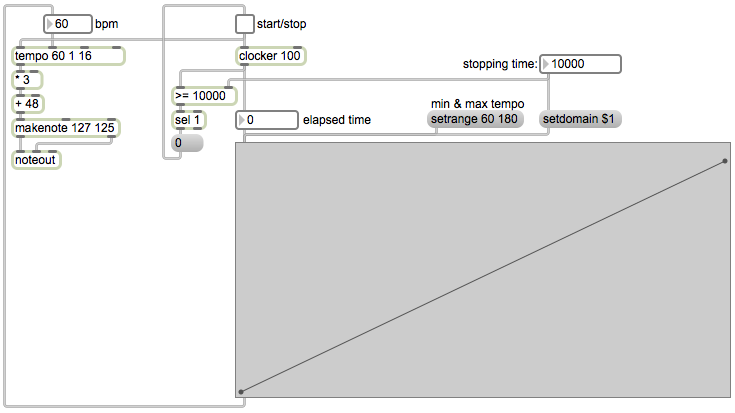
The function object in this patch has been saved with its domain set at 10,000 and its range set from 60 to 180. Click on the toggle to see and hear what this patch does. When the toggle is turned on, it sends out the number 1, which turns on the clocker object, which in turn begins to report the time that has elapsed (starting at 0 at the moment it’s turned on) at regular intervals specified by its argument (every 100 milliseconds in this case). The elapsed time is used to look up a tempo between 60 and 180 in the function object, and that tempo is sent to the tempo object to determine its (quarter note) beats per minute. The elapsed time value from the clocker is also used to check whether the stopping time has been reached, which initially is 10,000 milliseconds. Finally, the 1 from the toggle will be used to start the tempo object, which will have already received the correct tempo from the function. When clocker reaches 10,000, the >= object will send out the number 1, which will be detected by the sel 1 object, which will turn off the clocker and the tempoobject. Thus, as the elapsed time progressed from 0 to 10,000 (or whatever you set as the stopping time), those increasing numbers read through the function that is in the lookup table, i.e., the line segment shape designating musical tempo that is in the function object.

The upper left portion of the patch is a very simple note generator. The tempo object is set to output numbers designating sixteenth notes at whatever quarter-note tempo it receives. The first argument is the initial tempo, and the next two arguments are the numerator and denominator of a fraction saying what kind of note value it should use as its output rate, in this case 1/16 notes. The tempo object will send out the numbers 0 to 15 showing which 16th note it’s on within a standard 4/4 meter. At the downbeat of each 4/4 measure, it wraps back around to 0 and repeats. Those numbers from the tempo object are multiplied by 3, thus counting by threes from 0 to 45, and then added to 48 so that it’s now counting by threes from 48 to 93. Those numbers 48, 51, 54, 57,…93 are used as pitch values in the makenote object, which combines them with a velocity value of 127 and sends 125-ms-long MIDI notes to the noteout object. The result is a four-octave arpeggiation of a C diminished seventh chord.

Try changing the domain of the function to play phrases of different durations. Try clicking in the function to create new points, making whatever shape of tempo changes you’d like to try. (You can shift-click on points to delete them.)

Linear mapping and linear interpolation

Image

lmap: Linear mapping equation

The term “mapping” refers to making a map of correspondences between a source domain and some other “target” range. (Think of the game where you are given words in one category and are challenged to try to find an appropriate correspondence in another category, as in “Kitten is to cat as puppy is to …”.) The simplest kind of numerical mapping is called “linear mapping”. That’s when a one-to-one correspondence is drawn from every value in a source range X to a value that holds an exactly comparable position in a target range Y. For example, in the target range 0 to 100, the value 20 holds exactly the same position as the value 2 does in the source range 0 to 10. In both cases, the value is 20% of the distance from the minimum to the maximum.

To convert one range into another linearly, there are really just two simple operations required: scaling (multiplication, to resize the range) and offsetting (addition, to push the range up or down). If you know the extent of two ranges X and Y, and a source value x, you can find the linearly corresponding target y value with this algebraic equation:
y = (((x-xmin)*(ymax-ymin))/(xmax-xmin))+ymin

This patch uses the expr object to implement that equation. In expr, the items such as $f1 and $f2 mean “the (floating point) number that has come in the first inlet”, “the (floating point) number that has come in the second inlet”, and so on. (Geeky technical note: We don’t need to use quite as many parentheses in the expr object as we did in the equation above, because the ordering of mathematical operations is implicit, due to the operator precedence that is standard in almost all programming languages.)

This patch has inlet objects and an outlet object so that it can be used as an object in another patch. You just save this patch with the name “lmap” somewhere in Max’s file search path, and you can then use it as a lmap object in any other patch. You establish the X and Y ranges by specifying their minimum and maximum (xmin, xmax, ymin, and ymax), then you send an x value in the left inlet to get the corresponding y value out the outlet. Thepatcherargs object supplies default initial values for xmin, xmax, ymin, and ymax in case no arguments are typed into the object when it’s created in the parent patch; however, if values are typed in for xmin, xmax, ymin, andymax (as in lmap 0. 1. -2. 2.), the patcherargs object inside lmap will send those values out instead of its default values.

Go ahead and download that patch and save it with the name “lmap”, as it will be used in the next example. In Max, patches that are saved with a one-word filename and used as objects in another patch are called “abstractions”. This lmap abstraction functions very much like the zmap object and scale object that already exist in Max, but I’ve provided lmap here so that you can see how one might implement the basic linear mapping function (in any language).

 

Linear mapping and linear interpolation

This patch shows examples of linear mapping and linear interpolation, using the lmap abstraction described above. One could substitute the built-in Max object scale in place of lmap with the same results.

As shown in the upper-left corner, with no arguments typed in lmap maps input values 0 to 127 (such as MIDI control data) into the range 0.0 to 1.0 (just as the scale object does by default). The output range 0.0 to 1.0 is useful for controlling the parameters of a lot of Jitter objects, and it’s also a range that can be re-mapped to any other range with simple scaling and/or offsetting (multiplication and/or addition).

Just below that is a mundane example of how linear mapping applies to common everyday conversion, such as converting temperatures from Fahrenheit to Celcius.

You can use linear mapping to step through any range in a specific number of N steps, just by setting an input range from 1 to N and providing input x values that count from 1 to N. This is demonstrated by the part of the patch labeled “go from A to B in N steps”. In effect, this is linear interpolation from A to B, since each step along the way will produce a corresponding intermediate value.

The part of the patch just above that demonstrates another case of the relationship between mapping and interpolation. The counter object counts cyclically in 360 steps from 0 to 359 (i.e., from 0 to almost 360), and we map the range 0 to 360 (the number of degrees in a circle) onto the output range 0 to 2π (the number of radians in a circle). Thus we’re able to go continually from 0 to (almost) 2π by degrees. (We then map that value with an inverse relationship in order to cause the dial to show the radial angle changing counterclockwise as it would be graphed in Cartesian trigonometry. Setting ymin to be greater than ymax causes such an opposite mapping.)

The Max objects line, line~, and bline offer three methods for linear interpolation within a single object.