Tag Archives: MIDI

Adjust pitches according to a pitch class set

Image

One potential use of the “inlist” abstraction is to compare incoming pitches to a pitch class set. This patch uses a % 12 object to find the pitch class of an incoming pitch, then compares it with the members of a prescribed pitch class set. If it belongs to the pitch class set, it gets passed on unchanged; if it doesn’t belong to the pitch class set, it gets pushed up one semitone and tested again.

Note that this patch does point to a potential bug (a so-called “screw case”). If the pitch class set is null (the bag inside the inlist abstraction is empty), any incoming pitch would set this patch into an infinite loop and cause a stack overflow. However, we’re safe in this particular example because we have pre-loaded the pitch class set and there’s no way provided in the program to delete those numbers.

MIDI-DMX conversion

Image

DMX data is encoded with “channel” information similarly to MIDI so that each receiving device can pay attention only to particular information. Each channel can carry a value from 0-255. Note that it’s therefore easy to convert the standard MIDI range 0-127 to the DMX range 0-255 just by multiplying values by 2 (or by shifting the number one bit to the left).

Bass drum player with swing

Image

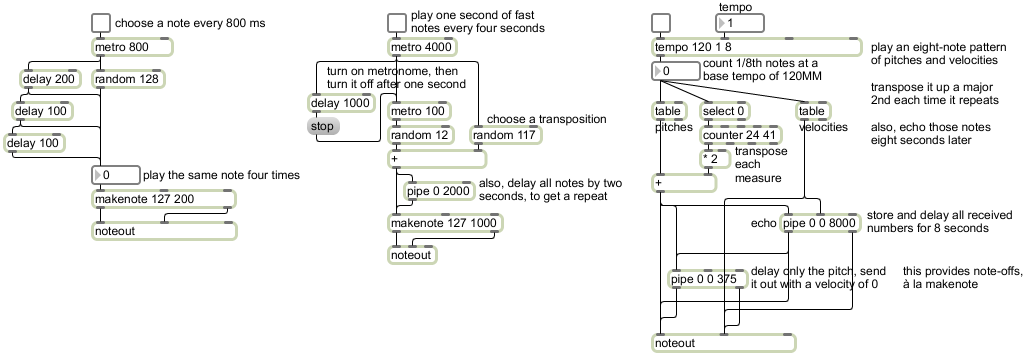
This patch uses the transport object to control an algorithmic performer of kick drum patterns. When the transport is turned on, the metro also turns on because its active attribute is set on. The metro sends a bang on every 16th note. Those bangs are first used to trigger information from the transport itself, and then to look up in a table of patterns to see whether or not to play a bass drum note. Along the way, the bangs from the metro pass through a subpatch that applies a certain amount of delay–equal to some proportion of a 16th note–to every other 16th note, giving a variable amount of “swing” feel to the drum patterns.

For each bang of the metro, we get information from the transport: the bar number, the beat number, and the number of units (ticks) within the beat. On the right part of the patch, you can see that we use the change object to filter out repetitions of bar number, so we will only pass on the bar number when it changes, which is to say, on the downbeat of each bar. We use that downbeat indicator to choose a random number from 0 to 7, and multiply that by 16 so that we get the numbers 0, 16, 32, … 112. That result gets stored in a +object. We’ll see what it’s used for in just a minute.

For now, let’s ignore the patcher swinger object. We’ll come back to that. Let’s imagine that the bang from the metro is just going directly to the patcher which16th. The metro sends a bang on every 16th note, and the patcher which16th subpatch will tell us which 16th note of the measure is occurring, using numbers 0 to 15. (Side note: you could also use a counter 0 15 object to generate that information, but if the transport time were to be changed in some other patch, the counter could get out of sync with the downbeat, and would be providing incorrect information.) Double-click on the patcher which16th object to see its contents. Since there are 480 divisions per quarter note by default, and the metro is quantized to occur only on 16th notes, the units coming in the right inlet will always be 0, 120, 240 or 360. So we divide by 120 to get which 16th note of the beat it is — 0, 1, 2, or 3. The beats coming in the middle inlet are numbered 1 to 4, so we subtract 1 and multiply by 4 to convert that to a number of 16th notes, add it to the 16th note offset from the units, and store the result in the right inlet of an i object. That’s the 16th note index within the measure, numbered from 0 to 15. Then, when the bang from the metro comes in an instant later, it will send out the correct 16th note index.

We use that 16th note index to look up information in the table object. But before it gets to the table, it passes through the + object where we previously — on the downbeat of each measure — stored some offset 0, 16, 32, …112. That means that for each measure, we will be looking up some different range of sixteen values in the table: 0-15, 16-31, 32-47, etc. up to 112-127. Double-click on the table object to see its contents. It stores 128 values ranging from 0 to 3. A table of 0s and 1s is useful for storing patterns of on/off information; in this case I decided to use numbers 0 to 3 so that the table could store four gradations: off, soft, medium, and hard. Every group of 16 values in the table is a unique composed rhythmic pattern of notes suitable as a kick drum rhythm in 4/4 time. Using the information derived from the transport, we read through a group of 16 articulation values to get one of 8 possible rhythmic patterns. The output of the table will always be numbers 0 to 3, which we use to trigger velocity values: 80, 104, 127, or no action (for 0). Those velocity values are passed to a noteout object that’s set to transmit on MIDI channel 10 — the channel designated for drums in the General MIDI specification — and then a pitch value of 36 — designated to mean kick drum in the GM specs — is sent to noteout to trigger the note.

Now let’s take a look at the patcher swinger subpatch. As you know, in various styles of jazz and popular music, 16th notes are played unevenly, with the duration of the first of each pair of 16ths being slightly longer than the second. You might just as well say that the onset time of the second of each pair of 16th notes is delayed slightly. This practice is known as “swing”. Scientific musicologists who have studied the performance of music that involves swing have found that the amount of swing varies from one style of music to another, and is also dependent on the tempo of the music. So, rather than try to quantify swing as some particular rhythmic unit, such as a triplet 8th note, it may make more sense in computer music to quantify swing as some percentage of a beat, or of a half beat. That’s how we do it in this patch. If you figure that normally an unswung 16th note is 50% of an 8th note (120 ticks for a 16th, and 240 for an 8th), then a swung 16th note might range from 50% (no swing) to 75% (extreme swing equal to a dotted 16th note) of an 8th note. So to specify how much swing we want, I provide the user with a live.dial object that has a range from 50 to 75 and its units displayed with a % sign. Regardless of the range of the live.dial or how its units are displayed, however, its right outlet will always send a float value from 0 to 1 based on the dial position. Now double-click on the patcher swinger object to see its contents.

Inside the patcher swinger subpatch, the 0-to-1 value from the live.dial gets multiplied by 60 to produce some number from 0 to 60. The “ticks” value from the transport, which will always be 0, 120, 240, or 360 in this case, gets divided by 120 to convert those numbers to 0, 1, 2, or 3. We then use a bitwise operator & 1 to look just at the least significant bit of that number (the 1s place of its binary representation) to see if the number is odd or not. If the number is odd, the & 1 object will send out a 1; if not, it will send out a 0. That gets multiplied by the number from 0 to 60 we got from the right inlet, gets packed together with the word “ticks”, and is stored in the right inlet of the delay object as a tempo-relative time value. It’s the number of ticks we want to delay each 16th note: 0 delay for even numbered 16ths and some amount of delay for the odd numbered 16ths. (Remember, we’re indexing the 16th notes of the measure starting from 0.) 0 ticks is no delay, and 60 ticks is a 32nd note’s worth of delay. So each bang that comes in the left inlet gets delayed by some amount, depending on whether it’s the first or second of a pair of 16ths, and based on the amount (percentage) of swing specified in the main patch.

I worked with only the kick drum in this example, so that the patch would not become too complicated, but one could duplicate this procedure for all of the other instruments of the drum kit, with unique patterns appropriate to each instrument, to get a full constantly-varying automated drum performance.

Note that this patch requires virtually no modification to work as a MIDI plug-in in Ableton Live. One can copy and paste this patch into Max for Live, add the “Swing” live.dial to the Presentation, move it to the visible area of the Presentation (the upper left corner), and set the patcher to “Open in Presentation” in the Patcher Inspector. The control messages to the transport object would become superfluous because the Live transport would be in charge, but the bang messages to the transport object from the metro will still report the correct time so that the patch will work as it should. The swing function will have the same effect, and will be independent of any “Groove” setting the Live track might have.

Time interval and rate

Image

This patch provides examples that compare linear rate changes to exponential rate changes. As with pitch and loudness, our sense of change in the rate of events is based on the ratio of tempos rather than the (subtractive) difference between tempos. In these examples, the rate changes by a factor of 16, from 1 event per second to 16 events per second, or vice versa. In the first example, we use a linear change of time interval for a metro, to go gradually from 62.5 milliseconds to 1000 milliseconds, which is to say from 16 notes per second to 1 note per second. By changing the time interval linearly, we get a larger change in the notes-per-second rate initially than we do later in the accelerando, which means that most of the change in perceived tempo takes place in the earliest part of the thirty seconds. In the second example, by contrast, we use line to effect a linear change in the notes-per-second rate (tempo), which actually causes an increasing rate of change in the time interval being provided to metro, but results in an accelerando that seems (and in fact is) more constant over the course of the thirty seconds, and is thus more musically useful. In the two examples on the left the change, be it of time interval or rate, is linear. In the two examples on the right, the output of line objects is used as the exponent in a pow object, thus converting the linear rate change into an exponential one. This yields, in most cases, a smoother and more “musical” sense of accelerando or decelerando. Exactly which method of change you choose to use depends on which most closely corresponds to the musical effect you’re trying to achieve.

MIDI and audio via ReWire

Image

Max can interface with other applications via ReWire. Max can act as either a ReWire host or a ReWire client. Max can be a client to an open host application just by choosing “ad_rewire” as the MSP audio driver in the DSP Status window. Alternatively, you can use Max as the host (mixer) application by including the rewire~ object in your program. This establishes Max as a mixer (host) application, and a ReWire-capable synth application that you open while Max is a mixer will pipe its audio to MSP via the outlets of the rewire~ object.

This example shows Max in use as a host to the synth program Reason. Max can send formatted MIDI messages to Reason to play notes and control parameters of the Reason devices (see the rewire~ reference page for details), and MSP can further process the synth audio after it comes out of rewire~. Here Max is generating note information, formatting it as MIDI messages and sending those to the rewire~ object to be transmitted to Reason via ReWire. The audio that Reason produces in response will be piped back to Max via ReWire, where it can be used in MSP. (In this case MSP is only being used to control the output volume, but the sound received via ReWire can be treated just like any other MSP audio signal.)

Routing MIDI to other applications

Image

The easiest way to establish MIDI connection between Max and other applications on the same computer is via the “virtual” MIDI ports Max provides. Max creates two virtual input ports and two virtual output ports that can be accessed by other MIDI applications. (You can see those virtual ports listed in Max’s MIDI Setup, by choosing MIDI Setup… from the Options menu.)

This example shows how one can generate MIDI information in Max and send it to another application. Here note information and controller information is being sent to the virtual port “from MaxMSP 1”. Any application that’s set to receive MIDI input from that virtual port will get the data that Max is transmitting. In this case Max is generating a cloud of random notes and is also moving the volume up and down in a sinusoidal fashion every 100 notes.

Delaying MIDI notes

Image

 

There are many objects available for delaying events (i.e., for scheduling events to happen at a specific future moment). For timing and scheduling events, the most common object is the metro object (send bang periodically at a specified time interval), which can be used to trigger events, start/stop entire processes, or trigger a counter to step through a table or a coll or any sort of sequence of things. To show the user the passage of time, the clockerobject is useful (report elapsed time periodically), as are timer (measure the time between two events) and tempo (count rhythmic units according to a metronomic tempo). For delaying a single bang, use delay; for delaying one or more numbers, use pipe; for delaying an audio signal, use delay~ or the variable delay line objects tapin~ and tapout~; for delaying a video, you would generally use jit.matrixset.

This patch contains a couple of simple examples demonstrating the use of delay and pipe (note that one is for bangs and one is for numbers), plus a slightly more complex example using tempo (to look up numbers in a table at a metronomic rate) and pipe (to echo the notes, and also to provide all the note-offs).

The first program, on the left side of the patch, chooses a number at random from 0 to 127 every 800 milliseconds and plays it as the pitch of a MIDI note. Each number gets displayed, and stored temporarily, in the numberbox. Each bang from metro that triggers a number also gets delayed by three different delay objects, and those delayed bangs trigger the same number in the number box a few tenths of a second later. What results is a 4-note rhythmic pattern for each pitch.

The second program, in the middle of the patch, illustrates a couple of important concepts. The first concept is that timing is an important aspect of a composition at many structural levels: microscopic (the sample level in audio or the frame level in video), small formal level (notes in music or edits in video), middle formal level (such as a phrase in music), or even at the global formal level (entire sections of a composition, scenes, etc.). Thus, a metroobject can be used to generate a very fast sequence of bangs to display frames of video or generate a smooth stream of events, and it can be set moderately fast to generate notes, but it can also be set to a much longer time interval to trigger phrases (sequences of notes or events) or to turn on and off entire complex programs. A second concept is that the same bang that triggers the start of a process can also be used to trigger a delay object to turn off the same process at some designated time in the future. Also, perhaps most commonly, delays can be thought of as echos or repetitions, either short-term or long-term, either verbatim or with some sort of variation.

At the top of the program is a slow metro that sends a bang every four seconds. The first thing it does is trigger a random number from 0 to 116, a “transposition” value to be stored as the right operand of the + object. Immediately after that, it turns on a faster metro, and it also triggers a delay object. The faster metro chooses random numbers from 0 to 11 at a rate of ten times per second. Those numbers get added to the randomly-chosen transposition value in the + object and used as MIDI pitch values by makenote. After one second of that, the delay object stops the fast metro, thus ending the “phrase” of fast notes. However, the fast pitch values are also all delayed by a pipe object that passes them on two seconds after they were generated, thus performing an echo of every randomly-generated phrase two seconds later.

The third program demonstrates the use of the tempo object, demonstrates the use of the table object, and also shows two uses of the pipe object.

The tempo object is like a combination of metro and counter, but it allows you to specify its rate in particular music-related terms. The first argument of tempo (or a number in its second inlet) specifies its tempo, in quarter notes per minute. The help file and manual page say that the tempo refers to “beats per minute”, but it’s really much more correct to say that it refers to quarter notes per minute. That’s because tempo is biased toward 4/4 meter. It thinks of a measure always as being a whole note, and its tempo refers to the rate of a quarter note. The next two arguments (inlets) are for specifying a “multiplier” and “division”, which are probably best thought of as the numerator and denominator of the fraction of a whole note that you want tempo to use as its actual rate of output. For example, in this program, we have specified a tempo (a quarter note rate) of 120 bpm, and we’ve askedtempo to report 1/8 notes. At a quarter note rate of 120, we would expect eighth notes to occur at a rate of 240; that is, if quarter notes occur every 500 ms, eighth notes occur every 250 ms. This tempo object thus outputs at a time interval of 250 ms, and counts the eighth notes in the 4/4 measure, starting at 0 (as computers often do) and counting up to 7 over the course of a measure. This is comparable to using a metro 250 object to bang a counter0 7 object.

We use the output of tempo to look up some stored information in two table objects. The table object is what’s commonly called a “lookup table” or an “array”. You can store an ordered array of numbers, and then look up those numbers by referring to their “index” number (also sometimes called the “address”) in the array. In table, the index numbers start from 0, and each location in the array can hold an integer. In the table‘s Inspector, you can set it to save its contents as part of the patch, so that the stored numbers will always be there the next time you open the patch. When table receives an index number in its left inlet, it sends out the number that is stored at that index location. In this patch, we use one table to store an 8-note pattern of MIDI velocities, and we use another table to store a pattern of pitches. (You can double click on the table objects to see their contents displayed graphically.)

Each time the tempo object sends out the number 0, which is to say at the beginning of each “measure”, each cycle of 8 eighth notes, we use a select object to detect that fact, and we trigger a new transposition for the pitch values. The counter object is set to count from 24 up to 41, but its output is then multiplied by 2, so in effect it’s actually counting upward by twos, from 48 to 82. Those numbers are used as the base key, the transposition, for the simple melodic pattern contained in the pitch table. Note that the pitch pattern in the table was composed so as to outline an upward tonic major 7 chord followed by a downward secondary dominant 7 chord (V65/ii), thus leading directly into the next iteration which will be transposed a major 2nd higher.

These pitches and velocities are sent to a noteout object to be transmitted as MIDI note-on messages. Each pitch (but not the velocity) is also sent to a pipe 0 0 375 object so that it, along with a 0 representing a note-off velocity, will be sent out 375 ms later to turn each note off. This has a comparable effect to using a makenote object. The pitches and velocities are also sent to a pipe 0 0 8000 object before going on to the other pipe andnoteout, which results in a verbatim repetition of all the notes 8 seconds later.