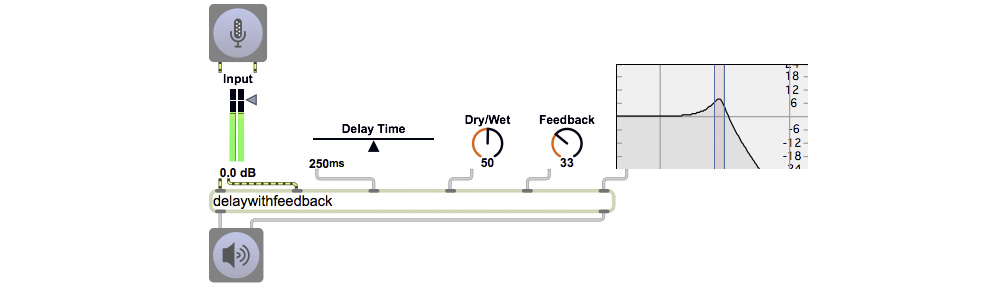
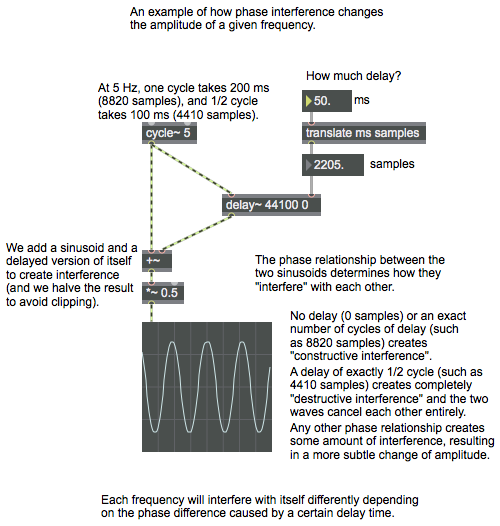
Some interesting effects can be obtained by feeding the output of a delay line back into itself and adding that to whatever new sound is coming in. The result is delays of delays, echoes of echoes, etc. As was shown in the discussion of Comb filtering, short delays fed back at a specific rate will have a strong resonance effect on the timbre of a sound. A filter that uses feedback of short-time delayed sound is called a recursive filter. Recursion is the process of applying a procedure to the result of that same procedure. It’s sometimes useful in programming, but it’s only possible in Max if a suitable amount of time is allowed to elapse so that the program doesn’t get into an infinite, unbreakable loop.
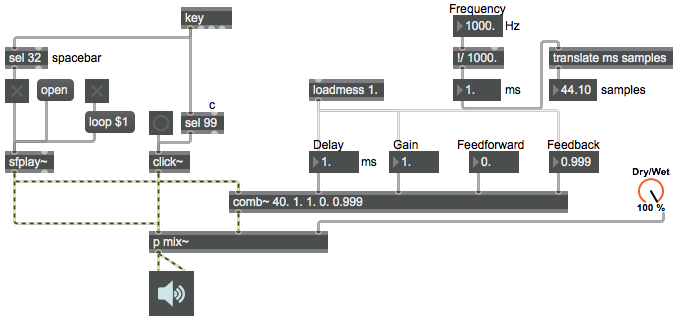
So there’s a problem with feedback in MSP. If an MSP signal chain included the necessity to have its own output in order to calculate its own output, you can see how that would be impossible (or would require an infinite amount of time). However, MSP calculates audio in “chunks” or “vectors” composed of several samples at a time (usually some power of 2, such as 64 for example, which would be just under 1.5 milliseconds assuming a sampling rate of 44,100 Hz). That means that if we’re willing to wait until at least one vector of samples has been calculated and sent out, we can use delay feedback. (Filter objects such as reson~ can use a shorter feedback time, because the object itself stores the fed-back information internally from one signal vector to the next.)
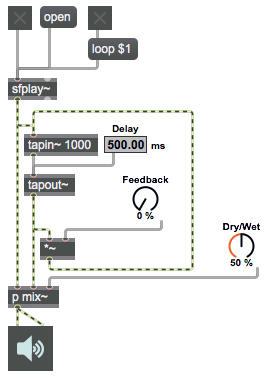
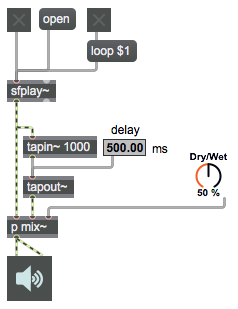
The tapout~ object has a minimum delay time equal to one signal vector’s worth of samples. No shorter delay is possible with tapout~, but the advantage of setting that minimum is that you can feed tapout~‘s output back into the input of its associated tapin~ object and it will have at least a one-vector delay to avoid an infinite loop of recursive calculation.
You will always want to scale the feedback signal down by some amount between 0 and 1 in order to ensure that the total amplitude (the sum of original plus feedback) doesn’t increase beyond the range of clipping. Here we use the right outlet of a live.dial object to provide an amplitude-scaling number from 0 to 1.