This example shows interference between two sine tones that have nearly the same frequency, causing a beating effect. One sine tone is kept at a constant frequency, while the frequency of the other oscillator is continuously modulated up and down by up to 12 Hz, using the technique shown in the previous example, “Modulating oscillator“. The two sine tones are added together, and they interfere at a rate equal to the difference between their two frequencies, causing the sense of beating at that rate.

sinemodulation.maxpat

If you set the modulating oscillator’s frequency to 0, it will stop wherever it is, and the difference between the two tones will remain constant. If you set the modulating oscillator’s amplitude to 0, its effect will be nullified, and the two sine tones will be in unison at 440 Hz.

Note that the amplitude of each of the two tones is set to 0.5 so that the sum of the two amplitudes will never exceed 1, which would cause clipping.

An oscillator is an electronic circuit that generates a cyclic (periodically repeating) signal. Classic examples of oscillator signal patterns include a sinusoidal signal (one that goes smoothly back and forth between two extremes, as a pendulum does in the physical world) or a square wave (one that switches instantaneously back and forth between two extremes, like an on-off switch).

In digital audio, we continue to use the term “oscillator” to refer to a program that generates a cyclically repeating audio signal. In MSP, an example of an oscillator is the phasor~ object, which ramps repeatedly from 0 to (almost) 1, like an ideal sawtooth pattern, at whatever rate of repetition you specify. Another commonly used example is the cycle~ object, which generates a sinusoidal signal with a peak amplitude of 1 at whatever frequency is designated. The way cycle~ actually works internally is that it uses a stored lookup table containing one full cycle of a cosine waveform, and it uses a phasor-like sawtooth pattern from 0 to (almost) 1 to scan repeatedly through that table at the desired frequency and send out the result. (You can also use cycle~ to scan repeatedly through a waveform stored in a buffer~ to produce any arbitrary cyclical signal, but for now we’ll just concern ourselves with its default behavior, which is to generate a sinusoid.)

A modulating oscillator is one that we don’t listen to directly, but instead we use its output to control some feature of the sound we do want to hear. Usually (but not necessarily) we set the frequency of the modulating oscillator to a sub-audio rate so that we can perceive its signal shape as it influences some other sound. For that reason, the modulating oscillator is often called a low-frequency oscillator, or LFO. A classic usage of an LFO is to modulate the frequency input of another oscillator that we do want to listen to. That’s called frequency modulation, or FM, and it’s demonstrated and explained in MSP Tutorial 10: Vibrato and FM, as well as in this example.

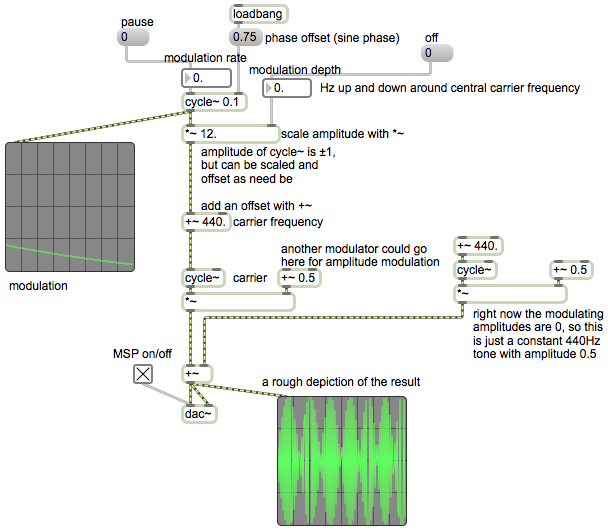
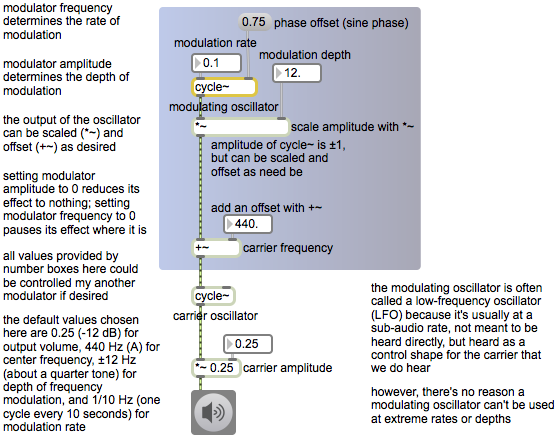
Normally we want to control at least three aspects of an LFO: its frequency (rate of repetition), its amplitude (the range or “depth” of its modulating effect), and an offset (a constant value added to it to move it into the desired range). Those values could be constant, or they could be changing continuously. (Indeed, they could potentially even be supplied by another LFO.) For this example we use constant values.

This example patch shows one cycle~ object being used as an LFO (the modulating oscillator) and another cycle~ object being used as the sound source (the carrier oscillator). The portion of the patch that’s inside the colored box shows how to use cycle~ as the modulator, using number boxes to specify the desired frequency, amplitude, and offset.

modulatorexample.maxpat

Note that the carrier oscillator’s frequency is controlled by a signal (not by typed-in argument or a Max message), which is the sum of a constant value (the offset) of 440, which you can think of as the center or base frequency, and the output of the modulating oscillator, which modifies that base frequency. The range, or depth, of that modulation is determined by the amplitude of the modulator, ± 12 in this case, so the frequency of the carrier will vary continuously between 428 Hz and 452 Hz, which is roughly ± one quarter tone variation of the central frequency. The rate of the variation is quite slow here, 0.1 Hz, meaning that a full cycle of the modulating waveform will occur once every ten seconds. Try other frequencies and amplitudes for the modulator to get an idea of the kind of frequency modulation effects that are possible.

The phase offset value of 0.75 supplied in the right inlet of the modulating cycle~ object means that when audio is turned on, that cycle~ will start 3/4 of the way through its waveform. Since its stored waveform is a cosine, starting 3/4 of the way through that cosine will cause it to start at a value of 0 instead of 1, and it will have a sine phase shift.

The sigmund~ object is a third-party object for pitch tracking designed by Miller Puckette and Ted Apel, available on their page of downloadable Max objects. You’ll need to have it installed for this example to work. Why is it called sigmund~? ‘Cause it’s your analyst, I assume! You might also want to have downloaded ducker~.maxpat from the previously posted example, so you can try it out in conjunction with sigmund~.

sigmunddemo.maxpat

To have sigmund~ attempt to discern discrete notes rather than give a continuous pitch evaluation, use the ‘notes’ argument. Pitches are reported using MIDI-based numbering, but using float values to show fractions of semitones. In most cases, it works better to round those values rather than truncate them, for more accurate representation of the intended pitch.

[This example has been determined faulty and is thus deprecated by its author. It’s left here merely for reference, but will not produce optimal results in actual use. A better ducker~ is presented as an example for Music 215B, winter 2016.]

A “ducker” is a system that turns a signal down to 0 when it’s below a given threshold. It’s useful for suppressing unwanted low-level audio, such as in a cell phone transmission when the user is not talking. Or, more to the point for musical purposes, as in a microphone signal when the musician is not playing.

ducker~.maxpat

In this patch the user specifies an amplitude threshold, attack time, and release time, either by sending those values in the appropriate inlets or by typing them in as arguments to the object in the main patch.

When the amplitude of the signal coming in the left inlet goes above the threshold, the >=~ object sends out 1, so the rampsmooth~ object starts heading toward 1 in the number of samples specified (i.e., starts fading in the signal). So as not to lose too much of the wanted signal, that fade-in should be quick. A good attack time might be in the range of 5-40 ms, depending on the source. When the amplitude of the signal coming in the left inlet goes below the threshold, the >=~ object sends out 0, so the rampsmooth~ object starts heading toward 0 in the number of samples specified (i.e., starts fading out the signal). For many instruments, the release time might be slower than the attack time, so you might want that fade-out time to be longer than the fade-in time. A good release time might be in the range of 200 ms or more, depending on the source.  In the main patch you can use the mstosamps~ object to calculate the correct number of samples for the fade times.

DMX data is encoded with “channel” information similarly to MIDI so that each receiving device can pay attention only to particular information. Each channel can carry a value from 0-255. Note that it’s therefore easy to convert the standard MIDI range 0-127 to the DMX range 0-255 just by multiplying values by 2 (or by shifting the number one bit to the left).

MIDI-DMX.maxpat