An oscillator is an electronic circuit that generates a cyclic (periodically repeating) signal. Classic examples of oscillator signal patterns include a sinusoidal signal (one that goes smoothly back and forth between two extremes, as a pendulum does in the physical world) or a square wave (one that switches instantaneously back and forth between two extremes, like an on-off switch).
In digital audio, we continue to use the term “oscillator” to refer to a program that generates a cyclically repeating audio signal. In MSP, an example of an oscillator is the phasor~ object, which ramps repeatedly from 0 to (almost) 1, like an ideal sawtooth pattern, at whatever rate of repetition you specify. Another commonly used example is the cycle~ object, which generates a sinusoidal signal with a peak amplitude of 1 at whatever frequency is designated. The way cycle~ actually works internally is that it uses a stored lookup table containing one full cycle of a cosine waveform, and it uses a phasor-like sawtooth pattern from 0 to (almost) 1 to scan repeatedly through that table at the desired frequency and send out the result. (You can also use cycle~ to scan repeatedly through a waveform stored in a buffer~ to produce any arbitrary cyclical signal, but for now we’ll just concern ourselves with its default behavior, which is to generate a sinusoid.)
A modulating oscillator is one that we don’t listen to directly, but instead we use its output to control some feature of the sound we do want to hear. Usually (but not necessarily) we set the frequency of the modulating oscillator to a sub-audio rate so that we can perceive its signal shape as it influences some other sound. For that reason, the modulating oscillator is often called a low-frequency oscillator, or LFO. A classic usage of an LFO is to modulate the frequency input of another oscillator that we do want to listen to. That’s called frequency modulation, or FM, and it’s demonstrated and explained in MSP Tutorial 10: Vibrato and FM, as well as in this example.
Normally we want to control at least three aspects of an LFO: its frequency (rate of repetition), its amplitude (the range or “depth” of its modulating effect), and an offset (a constant value added to it to move it into the desired range). Those values could be constant, or they could be changing continuously. (Indeed, they could potentially even be supplied by another LFO.) For this example we use constant values.
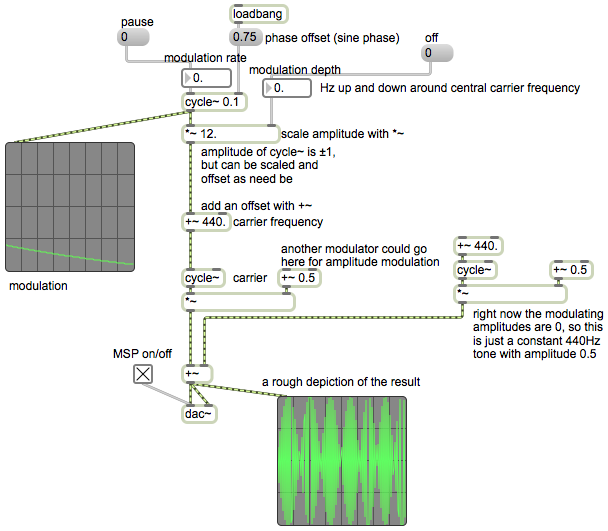
This example patch shows one cycle~ object being used as an LFO (the modulating oscillator) and another cycle~ object being used as the sound source (the carrier oscillator). The portion of the patch that’s inside the colored box shows how to use cycle~ as the modulator, using number boxes to specify the desired frequency, amplitude, and offset.
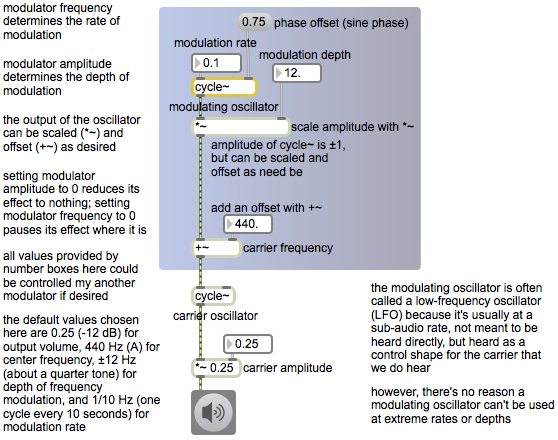
modulatorexample.maxpat
Note that the carrier oscillator’s frequency is controlled by a signal (not by typed-in argument or a Max message), which is the sum of a constant value (the offset) of 440, which you can think of as the center or base frequency, and the output of the modulating oscillator, which modifies that base frequency. The range, or depth, of that modulation is determined by the amplitude of the modulator, ± 12 in this case, so the frequency of the carrier will vary continuously between 428 Hz and 452 Hz, which is roughly ± one quarter tone variation of the central frequency. The rate of the variation is quite slow here, 0.1 Hz, meaning that a full cycle of the modulating waveform will occur once every ten seconds. Try other frequencies and amplitudes for the modulator to get an idea of the kind of frequency modulation effects that are possible.
The phase offset value of 0.75 supplied in the right inlet of the modulating cycle~ object means that when audio is turned on, that cycle~ will start 3/4 of the way through its waveform. Since its stored waveform is a cosine, starting 3/4 of the way through that cosine will cause it to start at a value of 0 instead of 1, and it will have a sine phase shift.