The MP3 Learning Object by Nathaniel Tull Phillips is a tutorial that describes the MP3 audio compression method.
Category Archives: Theory
Artificial intelligence and algorithmic composition
The development of computers, and devices that have computers embedded within them, has encouraged the exploration of machines that perform human actions. This exploration includes software that performs intellectual tasks, such as playing chess and composing music, and software-hardware systems that control machines robotically to perform physical tasks.
In the early years of modern computer development, mathematician and computer scientist Alan Turing developed ideas about computational algorithms and artificial intelligence. He hypothesized about the fundamental definition and nature of intelligence in his 1950 article “Computing Machinery and Intelligence“. In that article he proposed what eventually came to be known as the Turing test, which, if passed by a computer would qualify that machine as exhibiting intelligence. His premise can be paraphrased as implying that the appearance of human intelligence, if it is indistinguishable from real human behavior, is equivalent to real intelligence, because we recognize intelligence only by witnessing its manifestation. (This assertion was interestingly disputed by John Searle in his 1980 article “Minds, Brains, and Programs“.)
How can musical intelligence, as manifested in music composition, be emulated by a computer? To the extent that musical composition is a rational act, one can describe the methodology employed, and perhaps can even define it in terms of a logical series of steps, an algorithm.
An early example of a music composition algorithm is a composition usually attributed to Wolfgang Amadeus Mozart, the Musikalisches Würfelspiel (musical dice game), which describes a method for generating a unique piece in the form of a waltz. You can read the score, and you can hear a computer generated realization of the music. This is actually a method for quasi-randomly choosing appropriate measures of music from amongst a large database of possibilities composed by a human. Thus, the algorithm is for making selections from among human-composed excerpts—composing a formal structure using human-composed content—not for actually generating notes.
In the 1950s two professors at the University of Illinois, Lejaren Hiller and Leonard Isaacson, wrote a program that implemented simple rules of tonal counterpoint to compose music. They demonstrated their experiments in a composition called the Illiac Suite, named after the Illiac I computer for which they wrote the program. The information output of the computer program was transcribed by hand into musical notation, to be played by a (human-performed) string quartet.
Another important figure in the study of algorithmic music composition is David Cope, a professor from the University of California, Santa Cruz. An instrumental composer in the 1970s, he turned his attention to writing computer programs for algorithmic composition in the 1980s. He has focused mostly on programs that compose music “in the style of” famous classical composers. His methods bear some resemblance to the musical dice game of Mozart, insofar as he uses databases of musical information from the actual compositions of famous composers, and his algorithm recombines fragmented ideas from thos compositions. As did Hiller and Isaacson for the Illiac Suite, he transcribes the the output of the program into standard musical notations so that it can be played by human performers. Eventually he applied his software to his own previously composed music to generate more music “in the style of” Cope, and thus produced many more original compositions of his own. He has published several books about his work, which he collectively calls Experiments in Musical Intelligence (which is also the title of his first book on the subject). You can hear the results of his EMI program on his page of musical examples.
Modular synthesizer terminology
In the 1960s Robert Moog developed a voltage-controlled modular synthesizer. It consisted of a collection of individual electronic modules designed to synthesize sound or alter sound, and those modules could be interconnected in any way desired by using patch cords to connect the output of one module to the input of another module. The user could thus establish a “patch”—a configuration of interconnections for the modules—to create a unique sound, and could then play notes with that sound on a pianolike keyboard that put out voltages to control the frequency of the sound.
I’ll describe a few of the module types that were commonly found in such a synthesizer.
An oscillator is a circuit that creates a repetitively changing signal, usually a signal that alternates back and forth in some manner. That repeating oscillation is the electronic equivalent of a vibration of a physical object; when the frequency of the oscillation is in the audible range it can be amplified and heard. The oscillators in the Moog synthesizer were voltage-controlled, meaning that the oscillation frequency could be altered by a signal from another source.
Electronic oscillators often created certain specific types of waveforms, which were so common that they have come to be known as “classic” waveforms. The most fundamental is the sinusoid (a.k.a. sine wave), which is comparable to simple back-and-forth vibration at one particular frequency. A second classic waveform is the sawtooth wave, so named because it ramps repeatedly from one amplitude extreme to the other, and as the waveform repeats it resembles the teeth of a saw. It contains energy at all harmonics (whole number multiples) of the fundamental frequency of repetition, with the amplitude of each harmonic being proportional to the inverse of the harmonic number. (For example, the amplitude of the 2nd harmonic is 1/2 the amplitude of the fundamental 1st harmonic, the amplitude of the 3rd harmonic is 1/3 the amplitude of the fundamental, and so on.) A third classic waveform is the square wave, which alternates suddenly from one extreme to the other at a regular rate. A square wave contains energy only at odd-numbered harmonics of the fundamental, with the amplitude of each harmonic being proportional to the inverse of the harmonic number. (For example, the amplitude of the 3rd harmonic is 1/3 the amplitude of the fundamental, the amplitude of the 5th harmonic is 1/5 the amplitude of the fundamental, and so on.) A fourth waveform, the triangle wave, ramps back and forth from one extreme to the other. It contains energy only at odd-numbered harmonics of the fundamental, with the amplitude of each harmonic being proportional to the square of the inverse of the harmonic number. (For example, the amplitude of the 3rd harmonic is 1/9 the amplitude of the fundamental, the amplitude of the 5th harmonic is 1/25 the amplitude of the fundamental, and so on.)
An amplifier, as the name implies, serves to increase the amplitude of a signal. In a voltage-controlled amplifier, the amount of signal gain it provides to its input signal can itself be controlled by some other signal.
In a modular system, an oscillator might be used not only to provide an audible sound source, but also to provide a control signal to modulate (alter) some other module. For example we might listen to a sine wave oscillator with a frequency of 440 Hz and hear that as the musical pitch A above middle C, and then we might use a second sine wave oscillator at a sub-audio frequency such as 6 Hz as a control signal to modulate the frequency of the first oscillator. The first, audible oscillator is referred to as the carrier signal, and the second, modulating oscillator is called the modulator. The frequency of the carrier is modulated (altered up and down) proportionally to the shape of the modulator waveform. The amount of modulation up and down depends on the amplitude of the modulator. (So, an amplifier might be applied to the modulator to control the depth of the modulation.) This control of the frequency of one oscillator with the output of another oscillator is known as frequency modulation. At sub-audio rates such as 6 Hz, this frequency modulation is comparable to the vibrato that singers and violinists often apply to the pitch of their tone. The depth of the vibrato can be varied by varying the amplitude of the modulator, and the rate of the vibrato can be varied by varying the frequency of the modulator. When, as is often the case, the modulating oscillator is at a sub-audio control rate, it’s referred to as a low-frequency oscillator, commonly abbreviated LFO.
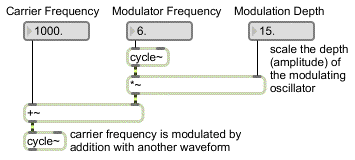
The diagram below shows schematically how a set of synthesizer modules might be configured to produce vibrato. The boxes labeled “cycle~” are sine wave oscillators, the box labeled “*~” is an amplifier, and the box labeled “+~” adds a constant (direct current) offset to a signal. In this example, the sine wave carrier oscillator has a constant signal setting its frequency at 1000 Hz, and that signal is modified up and down at a rate of 6 Hz by a sinusoidal modulator which is amplified to create a frequency fluctuation of + and – 15 Hz. The result is a sine tone centered on 1000 Hz with a vibrato going up and down 6 times per second causing a fluctuation between 985 and 1015 Hz.
A modulating LFO can also be applied to a voltage-controllable amplifier to create periodic fluctuations in the amplitude of a tone. This low frequency amplitude modulation is known in electronic music as tremolo. In electronic music we distinguish between the terms vibrato to describe periodic low-frequency frequency modulation and tremolo to describe periodic low-frequency amplitude modulation. (The Italian word tremolando means “trembling”. In instrumental music the words tremolo and tremolando are used to mean fast repetitions of a note, rather than subtle amplitude fluctuations. However, in electronic music the word tremolo is used to mean periodic change in loudness, similarly to the way vibrato is used to mean periodic changes in pitch. In vocal and instrumental music, vibrato is almost always synchronized with a corresponding fluctuation in loudness—which would be called tremolo in electronic music—thus further complicating the use of the term.)
Very slow frequency modulation can create a sense of the pitch gradually sliding. Sliding pitch is called glissando (an Italian musical term derived from the French word for sliding/gliding, glissant). In the sound example below, a sawtooth modulator LFO at a rate of 0.5 Hz is used to modulate the frequency of a carrier sawtooth oscillator, causing it to glide from 220 Hz to 440 Hz every 2 seconds. The same modulator also controls an voltage-controlled amplifier, which shapes the amplitude of the carrier so that it goes from loud to soft with each two-second glide.
An interesting possibility when using oscillators for modulating the frequency and/or amplitude of another oscillator is that the modulating oscillator might be amplified to produce very extreme fluctuations of pitch or loudness. Perhaps even more importantly, we can also vary the rate of the modulator from sub-audio rates (for classic LFO effects such as vibrato and tremolo) up into audio rates. When this happens, the modulation becomes so fast that we can no longer hear the effect as individual fluctuations, and the frequency modulation and/or amplitude modulation actually produces what are called sidebands—new frequencies that are related to the sum and the difference of the carrier and modulator frequencies, which are not present in the original oscillators themselves but which are generated by the audio-rate interaction of the modulator and the carrier. This can result in various strange and uniquely electronic sounds.
In the sound example below, the frequency of a sawtooth carrier oscillator is modulated by a sine wave LFO passing through an amplifier. At first the frequency of the LFO is sub-audio and its amplification is very low, so the effect is one of very subtle vibrato. Then the amplifier is turned up until the vibrato is extremely wide, making an inhuman warbling. Then the rate of the LFO is turned up until it is well into the audio range, so that we no longer hear it as a frequency fluctuation, but instead we hear many sidebands, creating a complex, inharmonic tone.
A filter is a circuit that can alter the timbre of a sound by reducing or increasing the amplitude of some of the sound’s frequencies. Common filter types are low-pass (pass low frequencies through unchanged, while reducing the amplitude of high frequencies), high-pass (pass high frequencies while reducing the amplitude of low frequencies), band-pass (pass or even emphasize a certain region of frequencies in the spectrum while reducing the amplitude of frequencies below and above that region), and band-reject (a.k.a. notch, to reduce the amplitude of a range of frequencies while passing through the frequencies above and below that region). Such filters can often be varied in terms of the frequencies they affect. Low-pass and high-pass filters are characterized by their cutoff frequency, the frequency at which they begin to substantially alter the frequency spectrum of a sound. For band-pass and band-reject filters, one more commonly refers to the center frequency, the frequency at the center of the affected band. A voltage-controlled filter can have its center frequency or cutoff frequency modulated by another signal source, such as an LFO. This can result in interesting and uniquely-electronic effects of timbre modulation, such as a a periodic filter vibrato or a gliding filter sweep. The sound example below is a 110 Hz sawtooth oscillator being passed through a low-pass filter; the cutoff frequency of the filter is at first being modulated by a sine wave LFO varying the cutoff frequency between 1540 Hz and 1980 Hz, and then the cutoff frequency is slowly swept down to 0 Hz.
We have discussed a few of the most significant types of voltage-controlled modules in the Moog modular synthesizer, such as oscillators, amplifiers, and filters. We’ve discussed four of the classic waveforms produced by the oscillators: sine, sawtooth, square, and triangle. These waveforms can be amplified and listened to directly, or they can be used as control signals to modulate the frequency of another tone. When we modulate the frequency of a tone at a sub-audio rate with a low-frequency oscillator (LFO), the resulting effect is called vibrato; when we modulate the amplitude of a tone (by modulating the gain level of an amplifier) at a sub-audio rate with a low-frequency oscillator (LFO), the resulting effect is called tremolo. Audio-rate modulation of the frequency and/or amplitude of an oscillator results in complex tones with sideband sum and difference frequencies. We’ve also discussed four common filter types: low-pass, high-pass, band-pass, and band-reject. Just as the frequency and the amplitude of a tone can be modulated, the cutoff frequency or center frequency of a filter can likewise be modulated by an LFO to create variations of timbre.
MIDI
By the late 1970s and early 1980s there were quite a few companies manufacturing voltage-controlled electronic synthesizers. Many of those companies were increasingly interested in the potential power of computers and digital communication as a way of providing control voltages for their synthesizers. Computers could be used to program sequences of numbers that could be converted into specific voltages, thus providing a new level of control for the synthesized sound.
In the early 1980s a consortium of synthesizers manufacturers—led by Dave Smith, founder and CEO of the Sequential Circuits company, which made the Prophet synthesizer—developed a communication protocol for electronic instruments that would enable instruments to transmit and receive control information. They called this new protocol the Musical Instrument Digital Interface (MIDI).
The MIDI protocol consists of a hardware specification and a software specification. For the hardware, it was decided to use 5-pin DIN plugs and jacks, with 3-conductor cable to connect devices. The cable establishes a circuit between two devices. Communication through the cable is unidirectional; one device transmits and the other receives. Thus, MIDI-capable devices have jacks labeled MIDI Out (for transmitting) and MIDI In (for receiving), and sometimes also a jack labeled MIDI Thru which transmits a copy of whatever is received in the MIDI In jack. MIDI communication is serial, meaning that the bits of information are transmitted sequentially, one after the other. The transmitting device communicates a digital signal by sending current to mean 0 and no current to mean 1, at a rate of 31,250 bits per second.
For the software specification, it was decided that each word of information would consist of ten bits: a start bit (0), an 8-bit byte, and a stop bit (1). Thus MIDI is theoretically capable of transmitting up to 3,125 bytes per second. A MIDI message consists of one status byte declaring what kind of message it is, followed by zero or more data bytes giving parameter information. In the next paragraphs discussing the actual contents of those bytes, we’ll ignore the start and stop bits, since they’re always the same for every byte and don’t really contain meaningful information.
A status byte always starts with the digit 1 (distinguishing it as a status byte), which means that its decimal value is in the range from 128 to 255. (In binary representation, an 8-bit byte can signify one of 256 different integers, from 0 to 255. The most significant digit is the 128s place in the binary representation.) A data byte always starts with the digit 0 (to distinguish it from a status byte), which means that its decimal value is in the range from 0 to 127.
What do the numbers actually mean? You can get a complete listing of all the messages in the official specification of MIDI messages. Briefly, there are two main categories of messages: system messages and channel messages. System messages contain information that are assumed to be of interest to all connected devices; channel messages have some identifying information coded within them that allows receiving devices to discern between 16 different message “channels”, which can be used to pay attention only to certain messages and not others. (A good metaphor for understanding this would be a television signal broadcast on a particular channel. Devices that are tuned to receive on that channel will pay attention to that broadcast, while other devices that are not tuned to receive on that channel will ignore it.) Let’s take a look at channel messages.
Channel messages are used to convey performance information such as what note is played on a keyboard, whether a pedal is up or down, etc. The types of channel messages include: note-off and note-on (usually triggered by a key on a pianolike keyboard), pitchbend (usually a series of messages produced by moving a wheel, to indicate pitch inflections from the main pitch of a note), continuous control (usually a series of messages produced by a fader, knob, pedal, etc., to describe some kind of curve of change over time such as volume, panning, vibrato depth, etc.), aftertouch (a measurement of the pressure applied to a key after it’s initially pressed), and program messages (telling the receiving device to switch to a different timbre). Rather than try to describe all of these in detail, we’ll look at the format of one particular type of message: note-on.
When a key on a synthesizer keyboard is pressed, two sensors at different heights underneath the key are triggered, one at the beginning and the other at the end of the key’s descent. Since the distance between the two sensors is known, the velocity with which the key was pressed can be calculated by measuring the time between the triggering of the two sensors. (v=d/t) The synthesizer clocks the time between the triggering of the two sensors to detect the velocity of the key’s descent. The synthesizer then sends out a MIDI note-on message telling which key was pressed and with what velocity.
A MIDI note-on message therefore consists of three bytes: message type, key number, and velocity . The first byte is the status byte saying, “I’m a note-on message.” Since the format of a note-on message is specified as having three bytes, the receiving device knows to consider the next two bytes as key number and velocity. The next two bytes are data bytes stating the number of the key that was pressed, and the velocity with which it was pressed. Let’s looks closely at the anatomy of each byte. (We’ll ignore the start and stop bits in this discussion, and will focus only on the 8-bit byte between them.)
A status byte for a note-on message might look like this: 10010000. The first digit is always 1, meaning “I’m a status byte.” The next three digits say what kind of message it is. (For example, 000 means “note-off”, 001 means “note-on”, and so on.) The final four digits tell what channel the message should be considered to be on. A receiving device can use the channel information to decide whether or not it wants to pay attention to the message; it can pay attention to all messages, or it can pay attention only to messages on a specific channel. Although these four digits together can express decimal numbers from 0 to 15, it’s conventional to refer to MIDI channels as being numbered 1 to 16. (That’s just a difference between computer numbering, which almost always starts at 0, and human counting, which usually starts at 1.) So, the four digits 0000 mean “MIDI channel 1”.
The first data byte that follows the status byte might look like this: 00111111. The first digit of a data byte is always 0, so the range of possible values that can be stated by the remaining seven digits is 0 to 127. By convention, for key numbers the decimal number 60 means piano middle C. The number shown in this byte is 63, so it’s indicating that the key D# above middle C is the key that was pressed. (Each integer designates a semitone on the equal-tempered twelve-tone chromatic scale, so counting up from middle C (60) we see that 61=C#, 62=D, 63=D#, and so on.) The next data byte might look like this: 01101101. This byte designates the velocity of the key press on a scale from 0 to 127. The number is calculated by the keyboard device based on the actual velocity with which the key was pressed. The value shown here is 109 in decimal, so that means that on a scale from 0 to 127, the velocity with which the key was pressed was pretty high. Commonly the receiving device will use that number to determine the loudness of the note that it plays (and it might also use that number for timbral effect, because many acoustic instruments change timbre depending on how hard they’re played).
So the whole stream of binary digits (with start and stop bits shown in gray), would be 010010000100011111110011011011. The first byte says, “I’m a note-on message on channel 1, so the next two bytes will be the key number and velocity.” The second byte says, “The key that was pressed is D# above middle C.” The third byte says, “On a scale from 0 to 127, the velocity of the key press is rated 109.” The device that receives this message would begin playing a sound with the pitch D# (fundamental frequency 311.127 Hz), probably fairly loud. Some time later, when the key is released, the keyboard device might send out a stream that looks like this: 010010000100011111110000000001. The first two bytes are the same as before, but the third byte (velocity) is now 0. This says, “The key D# above middle C has now been played with a velocity of 0.” Some keyboards use the MIDI note-off message, and some simply use a note-on message with a velocity of 0, which also means “off” for that note.
Notice that the MIDI note-on message does not contain any timing information regarding the duration of the note. Since MIDI is meant to be used in real time—in live performance, with the receiving device responding immediately—we can’t know the duration of the note until later when the key is released. So, it was decided that a note would require two separate messages, one when it is started and another when it is released. Any knowledge of the duration would have to be calculated by measuring the time elapsed between those two messages.
A complete musical performance might consist of very many such messages, plus other messages indicating pedal presses, movement of a pitchbend wheel, etc. If we use a computer to measure the time each message is received, and store that timing information along with the MIDI messages, we can make a file that contains all the MIDI messages, tagged with the time they occurred. That will allow us to play back those messages later with the exact same timing, recreating the performance. The MIDI specification includes a description of exactly how a MIDI file should be formatted, so that programmers have a common format with which to store and read files of MIDI. This is known as Standard MIDI File (SMF) format, and such files usually have a .mid suffix on their name to indicate that they conform to that format.
It’s important to understand this: MIDI is not audio. The MIDI protocol is intended to communicate performance information and other specifications about how the receiving device should behave, but MIDI does not transmit actual representations of an audio signal. It’s up to the receiving device to generate (synthesize) the audio itself, based on the MIDI information it receives. (When you think about it, the bit rate of MIDI is way too low to transmit decent quality audio. The best it could possibly do is transmit frequencies up to only about 1,500 Hz, with only 7 bits of precision.)
The simplicity and compactness of MIDI messages means that performance information can be transmitted quickly, and that an entire music composition can be described in a very small file, because all the actual sound information will be generated later by the device that receives the MIDI data. Thus, MIDI files are a good way to transmit information about a musical performance or composition, although the quality of the resulting sound depends on the synthesizer or computer program that is used to replicate the performance.
Definition of Technology
Technology means “the application of scientific knowledge for practical purposes” and the “machinery and equipment developed from such scientific knowledge.”
The word is derived the from Greek word tekhnologia, meaning “systematic treatment”, which is composed of the root tekhné, meaning “art, craft” and the suffix -logia, meaning “study (of)”.
In his book Understanding Media: The Extensions of Man (1964), Marshall McLuhan considered technology as a means of extension of human faculties, indeed as an extension of the human body beyond its physical limitations. Of course we use tools—the products of technology—to extend or amplify our physical capabilities. McLuhan pointed out that these extensions provided by technology and media can have both pros and cons.
Music Terminology
“Understanding” or “appreciating” music involves knowing something about the historical and cultural context in which the music was created (who made it? for whom was it made? how was it made? for what purpose was it used? etc.) and also requires having a methodology for analyzing sound, musical structure, and the experience of making and listening to music. Although some people may feel intuitively that everyone should be able to appreciate music naturally, without requiring special training, appreciation of music is actually both a visceral (emotional, gut-level) and an intellectual (rational, brainy) activity. Insofar as music appreciation is intellectual, it’s reasonable to believe that we can improve our appreciation through training and discussion.
One part of understanding music is having a framework of terminology to help us categorize and discuss musical phenomena. To that end let’s take a look at some terms that are used in the discussion and analysis of music, both instrumental and electronic. We can consider the meaning of these terms and can point to examples where the terms may apply.
Rhythm
Each sound is an event that marks a moment in time. We are capable of mentally measuring the amount of time between two events, such as between the onset of two sounds, thus we can mentally compare the time intervals between multiple events. This measurement and comparison process is usually subconscious, but we can choose to pay attention to it, and we can even heighten our capability with a little effort.
If sounds occur with approximately equal time intervals, we notice that as a type of repetition. (We notice that the same time interval occurred repeatedly.) That repetition is a type of pattern that gives us a sense of regularity, like the regularity of our heart beat and our pulse. When sounds exhibit a fairly constant beat or pulse (at a rate that’s not too fast for us to keep up with and not too slow for us to measure accurately in our mind), we are able to think of that as a unit of time, and we can compare future time durations to that unit. When something recurs at a fairly regular rate, we may say that it is periodic, and we refer to the period of time between repeating events. (The period is the reciprocal of the frequency of occurrence.) We’re able to use this period to predict when the next event in the series of repetitions is likely to occur.
We’re also capable of mentally imagining simple arithmetic divisions and groupings of a time period. For example, we can quite easily mentally divide a time interval in half, or multiply it by two, to calculate a new time interval, and we can notice when a time interval is half or twice the beat period.
With this mental measurement process, which allows us to detect arithmetically related time intervals, we can recognize and memorize patterns of time intervals. When we perceive that there is an organization or pattern in a sequence of events, we call that rhythm. We can find relationships between similar rhythms, and we can notice that rhythms are similar even when they are presented to us at a different speed. (A change of speed is also an arithmetic variation, in the sense that all the time intervals are multiplied by some constant value other than 1.) Musicians often refer to the beat speed as the tempo (the Italian word for time).
Pitch
We are able to discern different frequencies of sound pressure vibrations, and can compare those frequencies in various ways. When a sound contains energy at multiple frequencies, as is usually the case, if the frequencies are predominantly harmonically related (are whole number multiples of the same fundamental frequency) we perceive the sound as a unified timbre based on the fundamental frequency. We say that such sounds have a pitch, which refers to our subjective judgement of the sound’s fundamental frequency.
Most people are able to compare pitches, to determine which is “higher” or “lower”; that evaluation is directly related to whether a sound’s fundamental frequency is greater or lesser than that of another sound. With some practice, one can develop a fairly refined sense of relative pitch, which is the ability to identify the exact pitch difference between two pitched sounds; that evaluation is related to the ratio of the sounds’ fundamental frequencies. Thus, whereas we are mentally evaluating the ratio of two fundamental frequencies, we tend to think about it as a difference between two pitches. A geometric (multiplicative) series of frequencies is perceived as an arithmetic (additive) series of pitches.
Even when the sound is inharmonic, we’re sensitive to which frequency region(s) contain the strongest energy. So, with sounds of indefinite pitch, or even with sounds that are fairly noisy (contain many unrelated frequencies), we can still compare them as having a higher or lower pitch, in which case we’re really referring to the general pitch region in which they have the most sound energy. For example a small cymbal that produces mostly high frequency noise will sound higher in pitch than a larger cymbal that has more energy at lower frequencies.
So, even when we’re hearing unpitched sounds, we still can make pitch-based comparisons. A traditional musical melody is a sequence of pitched sounds, but a percussionist can construct a similar sort of melody made up of unpitched sounds, using instruments that produce noises in different pitch regions. Likewise, a musique concrète composer might use non-instrumental sounds of different pitch height to compose a “melody” of concrete sounds.
Motive
In various design fields, the term motif is used to designate the repeated use of a particular distinctive pattern, shape, or color to establish a predominant visual theme. In music composition the term motive (or motif) is used to describe a short phrase that has a distinctive pitch contour and a distinctive rhythm, which is then used repeatedly (with some variation) to create a sense of thematic unity over time. The distinctive aspects of the pitch contour and the rhythm make it easily recognizable to the listener, even when it has been modified in certain ways (such as using the original rhythm with a different pitch contour or vice versa). As the motive reappears in the music, the aspects that remain the same provide a sense of predictability and familiarity for the listener, and the motive’s distinctive traits provide a basis for variation that makes it useful for generating new-but-related ideas.
Counterpoint
Dynamics
Form
Gesture
Dialogue
Technological terms of editing and mixing recorded sound also become compositional ideas and techniques in music that is meant for recording (that is, music that was conceived to exist only as a recording, as opposed to the recording being simply a document of a live performance of the music).
Editing
Looping
Reversal
Fragmentation
Mixing
Panning
Echo
Binary number representation
Link
Computers calculate all numbers using binary representation, which means using only two digits: 0 and 1. If you’re not experienced with binary numbers, you might want to take a look at an online lesson on Representation of Numbers by Erik Cheever. Read at least the first two sections — “Introduction” and “Binary representation of positive integers”. (Keep reading beyond that if your brain can handle it.)
For the discussion of quantization of digital audio in this class, a key sentence in that lesson is “With n digits, 2n unique numbers (from 0 to 2n-1) can be represented. If n=8, 256 (=28) numbers can be represented 0-255.” How many different numbers can be represented by 16 digits? (The answer is provided right there on that page.)