Having begun the Age of the Higgs last year, which gives mass to all quarks and force particles except photons, we might expect that that is where most of our mass comes from. This is not the case, and we will show here how our mass comes about. It is from the confinement of colored quarks in nucleons of protons and neutrons. The part of the universe that we and the planets, stars and galaxies can see visibly is called ordinary matter. It is almost entirely made of nuclei of atoms consisting of protons and neutrons, and of electrons. The electrons do get their mass from the Higgs, but the electrons are only 1/2000 of the mass of the proton or neutron. The neutrons and protons are made up of very light quarks, called up and down quarks, which are less than 1% of the mass of neutrons or protons. So we must look at how quarks are confined in protons and neutrons to see where their mass or energy come from.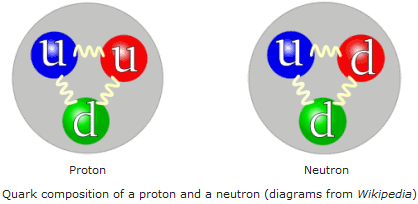 
Here are the pictures of the proton and neutron with the quarks that they contain, three for each of them.
We order our theories by the number of charges which they contain.
The oldest force we know (electricity and magnetism, or photons) couple to positive or negative electric charge. If the negative charge is that of the electron, the positive charge can be thought of as that of the antiparticle of the electron, called the positron.
In the weak isospin of the weak interactions, which we discuss elsewhere, there are two charges, which we call up and down. The antiparticles have charges called anti-up and anti-down. The charged W bosons make transitions between up and down quarks or leptons (electrons and neutrinos).
Quarks have one of three color charges, called red, green and blue. The antiquarks have charges anti-red, anti-green and anti-blue. When gluons are emitted or absorbed by quarks, similar to photons coupling to electrons, the gluons do more: they annihilate the color of the quark, and replace it with another or the same color of the original quark. So gluons act like color-anticolor pairs. There appear to be nine such combinations, but the symmetric (red-antired + blue-antiblue + green-antigreen) is actually colorless and does not couple to quarks or is not a real gluon. Thus there are only eight gluons. The theory of color charges and gluons is called Quantum Chromodynamics or QCD for short. Why is the name of color taken for the charges, since it has nothing to do with the real color of objects that are determined by the wavelengths of light? It is that the combination of red+green+blue mix to make white or colorless light.
Colored quarks or gluons have never been seen freely running around by themselves. This means that the color is confined inside nucleons or mesons, which from the outside are colorless combinations of quarks.
Mesons consist of a quark and an antiquark, in combinations of the above-mentioned form of (red-antired + green-antigreen + blue-antiblue), which makes the meson colorless.
A nucleon of three quarks combines (red + green + blue) to also make a colorless combination. This also means that there are no long-range color forces extending outside mesons or nucleons. How the confinement occurs is complicated because at low energies, or long distances, QCD becomes strong, and is not understandable in terms of simple Feynman diagrams that arise from weak interactions with only a few particles.
The oldest picture of confinement was of stretched rubber bands of color between the quarks that would take an infinite amount of energy to totally stretch far enough to maybe break. The energy stored with stretching to a distance r would be a constant times r, or kr, that is linear in r. The potential energy would be V_linear(r) = k r, a so called linear potential.
The exchange of gluons in colorless mesons leads to an attractive 1/r force, the same way the exchange of photons in an atom between oppositly charged protons and electrons leads to the attractive Coulomb potential 1/r, or V_electric(r) = − α_electric/r. So in QCD we get V_strong(r) = −4/3 α_strong/r. The sum of the strong potential energies V_QCD(r) = V_linear(r) + V_strong(r) forms the QCD potential. An actual calculation of this from the lattice method is shown below. The line labeled Cornell potential is the one we have put together as V_QCD(r). The negative potential at low r is the attractive one, and the linear rise at large r is the confining potential.
Classically, a particle in that potential would fall down the attractive potential at small r, if there was friction to lower its energy. Quantum mechanically, there will be a lowest state. This is an expression of the uncertainty principle between position and momentum. If a particle fell to small r, its radial momentum would become large, leading to high kinetic energy, leading to a higher energy. The minimum energy for a confined quark should be about 1/3 of the mc² of the nucleon, or about 1/3 of 938 MeV, or 313 MeV per quark. Since it is positive, the range of motion goes into the positive linear potential region.
So our mass, or that of protons and neutrons, is part kinetic energy, and part positive energy of colored stretched confining strings, offset in part by negative, attractive color gluon exchange. Aren’t you glad you know this now. There is a small amount of our mass generated by virtual gluons creating pairs of strange quarks and antiquarks, where these heavier strange quarks of about 150 MeV real mass gets their mass from the Higgs field non-zero vacuum value. This amounts to at most 3% of our mass. This is described in another post.
